1. Determine whether the equation x + (y + 1)^2 = 1 defines y as a function of x.

2.

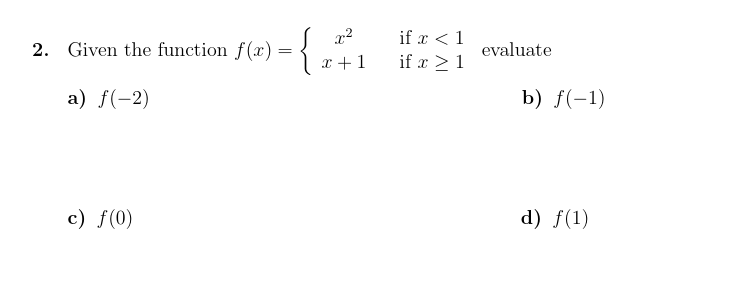
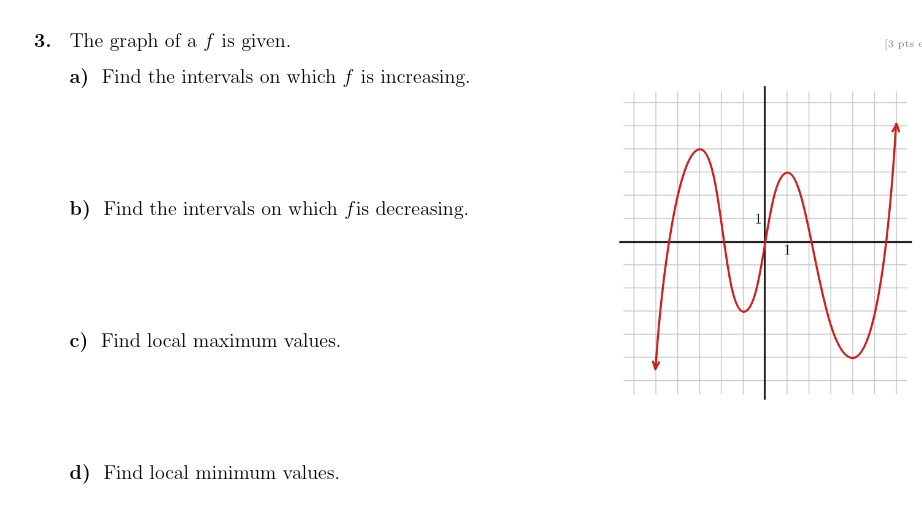
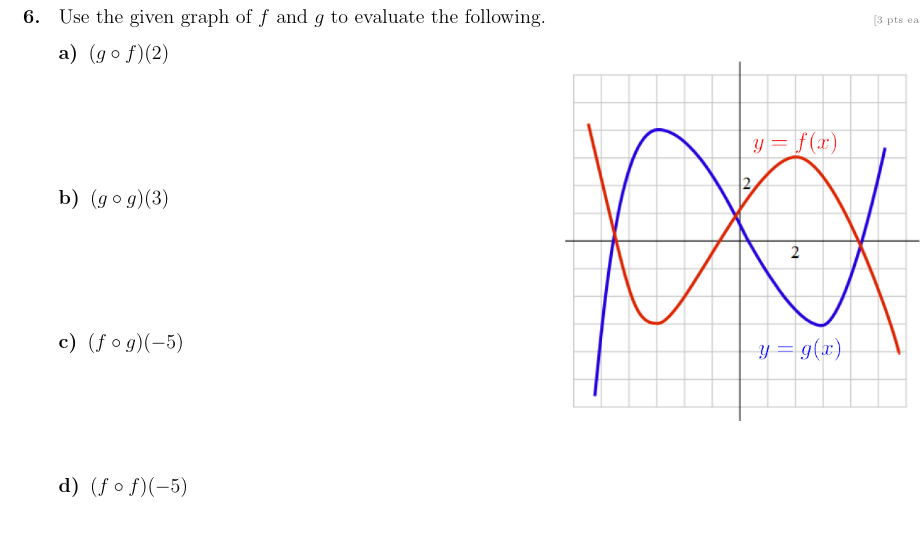
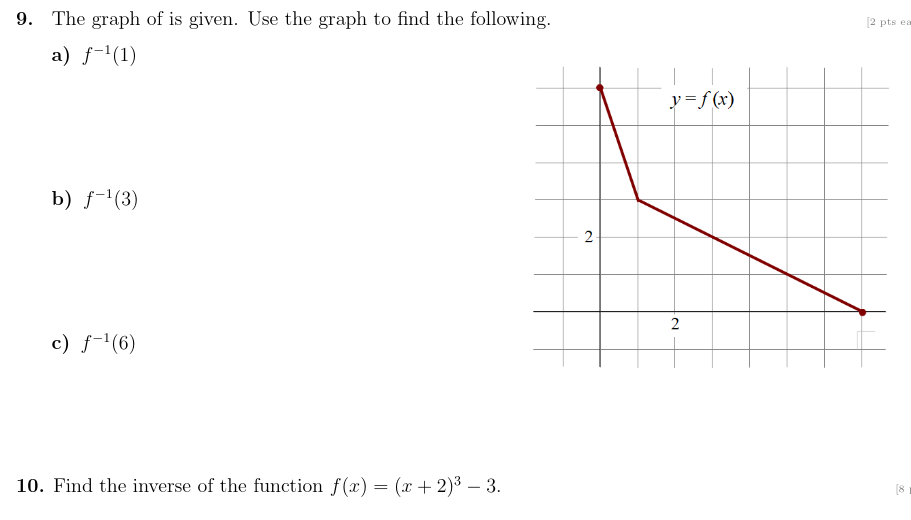
\fThe graph of a f is given. j-s pm a) Find the intervals on which f is increasing. [3) Find the intervals on which fis decreasing. c) Find local maximum values. d) Find local minimum values. 4. Write the equation of the nal graph obtained by applying the following transformations to the graph of f($) = 1:2. [W14 shift 4 units to the right and shift downward 2 units. 5. Find the domain of at} 2 m. [s \"15' . Use the given graph of f and g to evaluate the following. 33 W a) (9 0 W?) b) (9 o 9M3) C) (f Dan5] d) (f 0 f)(-5) 7. Given the functions f(x) =x2 -3 and g(a) = va, find the following. a) (fog)(x) b) (gof)(x) 8. Given H(x) = v1 -x2, find functions f and g so that H(x) = (fog) (x).9. The graph of is given. Use the graph to find the following. (2 pts ez a) f-1(1 ) y = f ( x ) b) f-'(3) 2 2 c) f-1(6) 10. Find the inverse of the function f(x) = (x + 2)3 - 3.11. Given the quadratic function f{$) = 2 + 4:: + 1 answer the following. j-._|+:_2j a] Find vertex (31.34:) and express the quadratic function in the form f{:l:) : afar Mg + k. b) Find four additional points on the graph and sketch it. x y c} Find its maximum or the minimum value. {State if it is man. or min.) (1) Find the domain and the range of f. Domain = Range 2 12. Find a polynomial of degree four whose graph is shown in the gure. ;a pm]