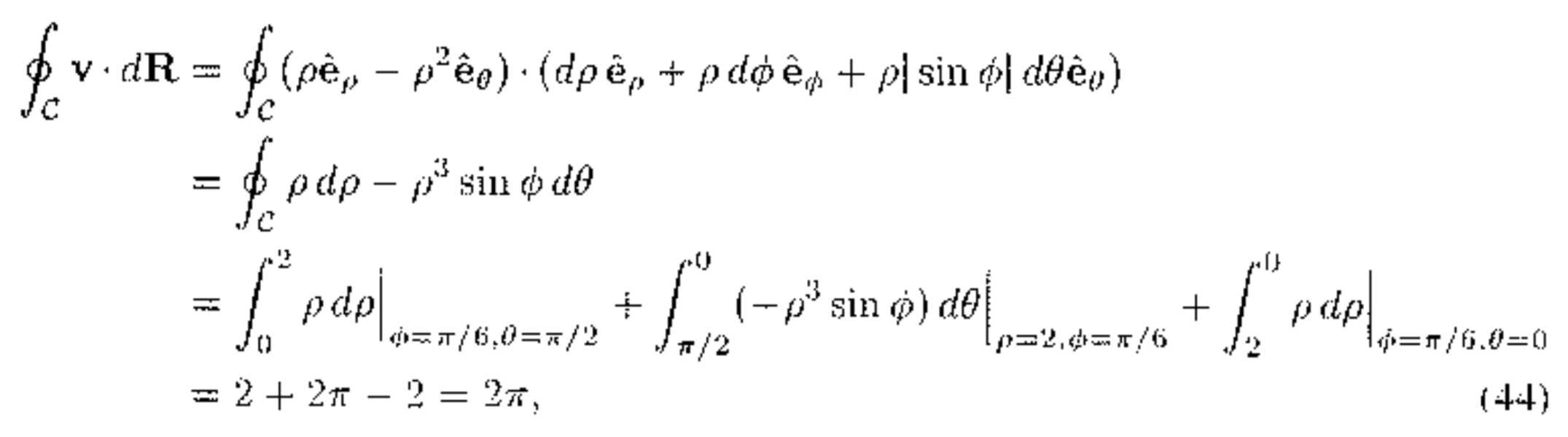
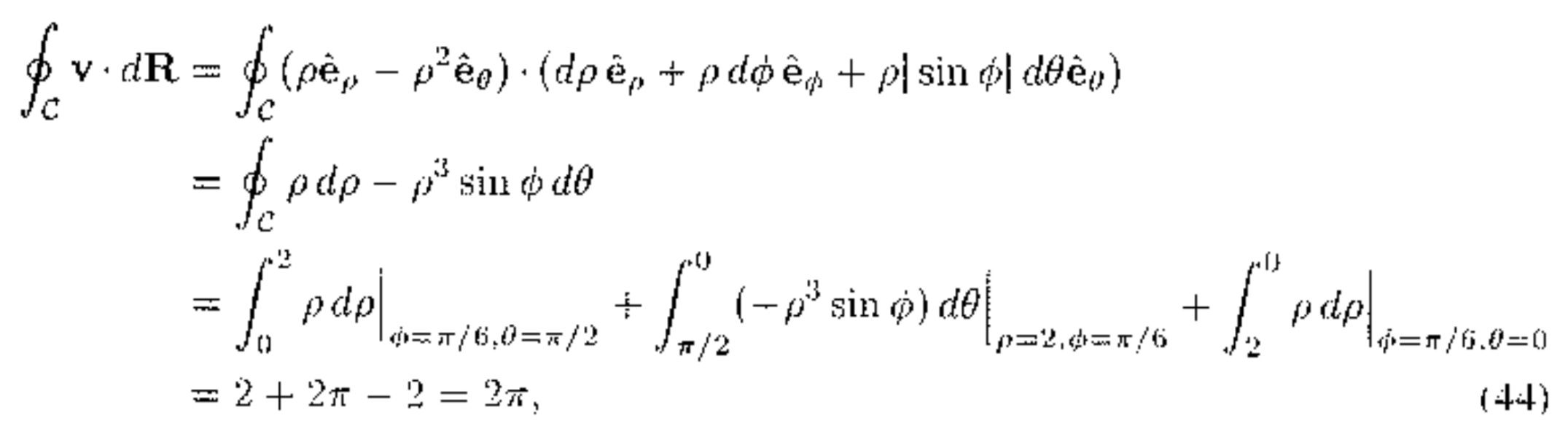
1. Evaluate Vu and V x Vu in each case. (h) u = sin (xyz) 2. Evaluate V . V x y and V x ( V x v) in each case. (Ov = fly)it gla)i 3. Are the parentheses needed in (14), i.e., in V x (V x v)? Explain. 4. Vu = 0 is called Laplace's equation. Show that the following are solutions of Laplace's equation. 1 (0) for a + y' + =2 0 5. If v is any vector. and R = xi + yj + sk, show that ( v . V )R = V. 6. Derive the following equations [as we have done in the text for (4) 1. (b) equation (6)1. In each case. verify the divergence theorem by working out fy V . vdV and fan . v dA and showing that the results are equal. (c) v = yi - 2j + ak. V: the rectangular prism |z) $ 2. 2. Let S be a piecewise smooth orientable closed surface en- closing a region of volume V. Show that (d) Isn (xi + yj + zk) dA = 3V 3. Verify Green's first identity (44) in each case. (b) u = 1, v = x2 + y' + 2", V: the cube 0