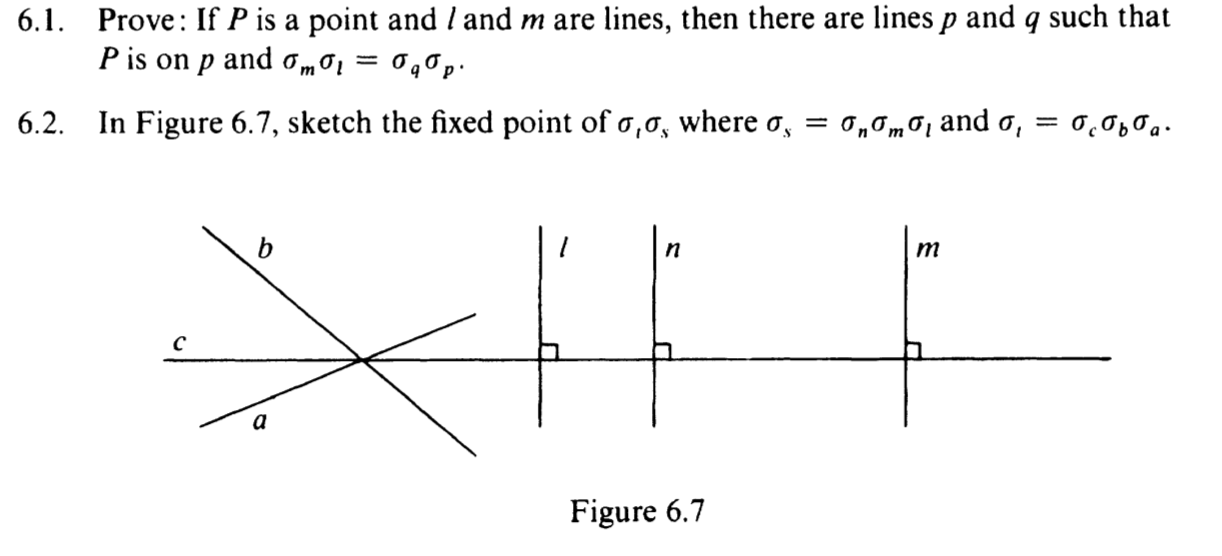
1. Exercise 5.1. Given AABC = ADEF, where A = (0,0),B = (5,0),C = (0,10),D = (4,2),E = (1,-2), and F = (12, 4), find equations of three or fewer lines such that the composition of reflections over the lines takes AABC to ADEF. Explain your work. You can use GeoGebra to illustrate, if you wish, but it is optional. 2. Exercise 5.3 (It is true, so prove.) Every isometry is either a product of five reflections or a product of six reflections. 3. Exercise 5.9 Prove that if o,, 0, fixes point P and m # n, then P is on both m and n. Hint: as a first step, show o,,(P) = 0,(P). 6.1. Prove: If Pis a point and / and m are lines, then there are lines p and such that Pisonpando,0, = 0,0,. 6.2. In Figure 6.7, sketch the fixed point of ,0, where o, = 0,0,,6,and g, = 07,0,0,. Figure 6.7