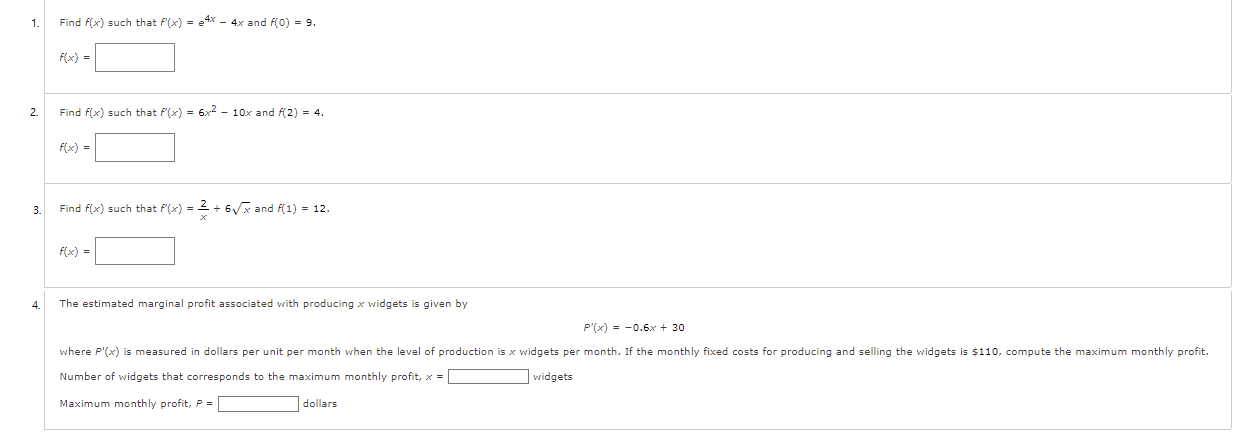
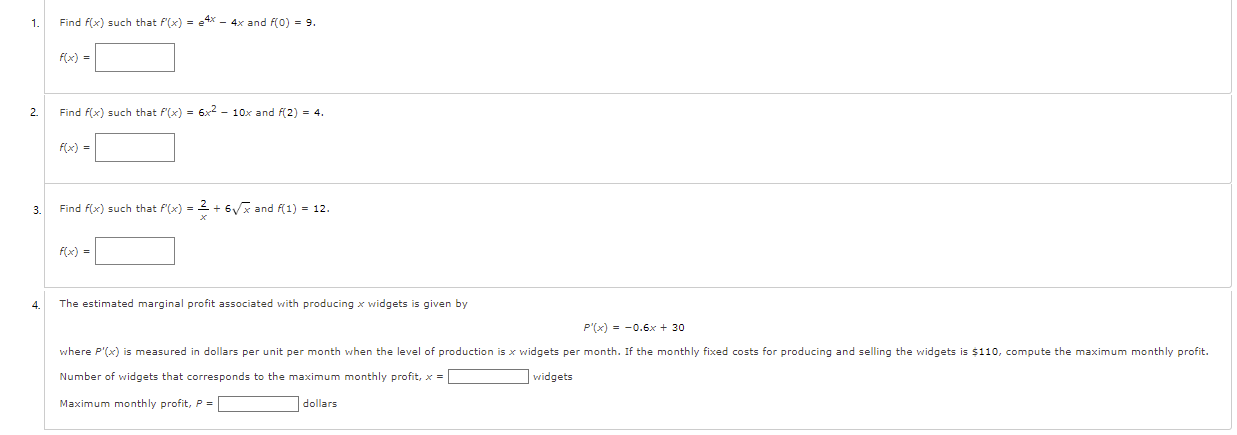
1. Find f(x) such that f(x) = e4* - 4x and f(0) = 9. F( x) = 2. Find f(x) such that f'(x) = 6x2 - 10x and /(2) = 4. F( x ) = 3. Find f(x) such that /(x) = _ + 6\\ x and f(1) = 12. F ( x ) = 4. The estimated marginal profit associated with producing x widgets is given by P'(x) = -0.6x + 30 where P'(x) is measured in dollars per unit per month when the level of production is x widgets per month. If the monthly fixed costs for producing and selling the widgets is $110, compute the maximum monthly profit. Number of widgets that corresponds to the maximum monthly profit, x = |widgets Maximum monthly profit, P = dollars