Question: 1. Find the exact area between the graph of e* + 12x and the x-axis on the interval [1,4]. | Let f(x) = %x'* %xz.
1.
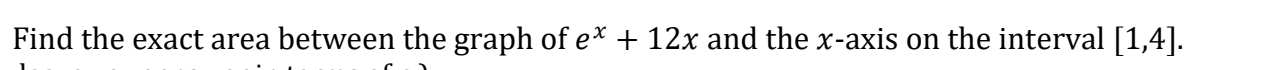
![and the x-axis on the interval [1,4]. | Let f(x) = %x'*](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/67098465314bf_9656709846512692.jpg)


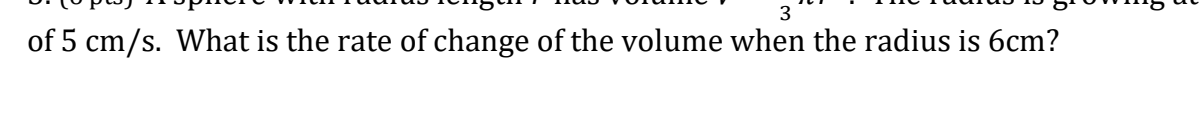
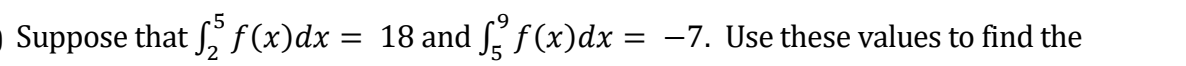
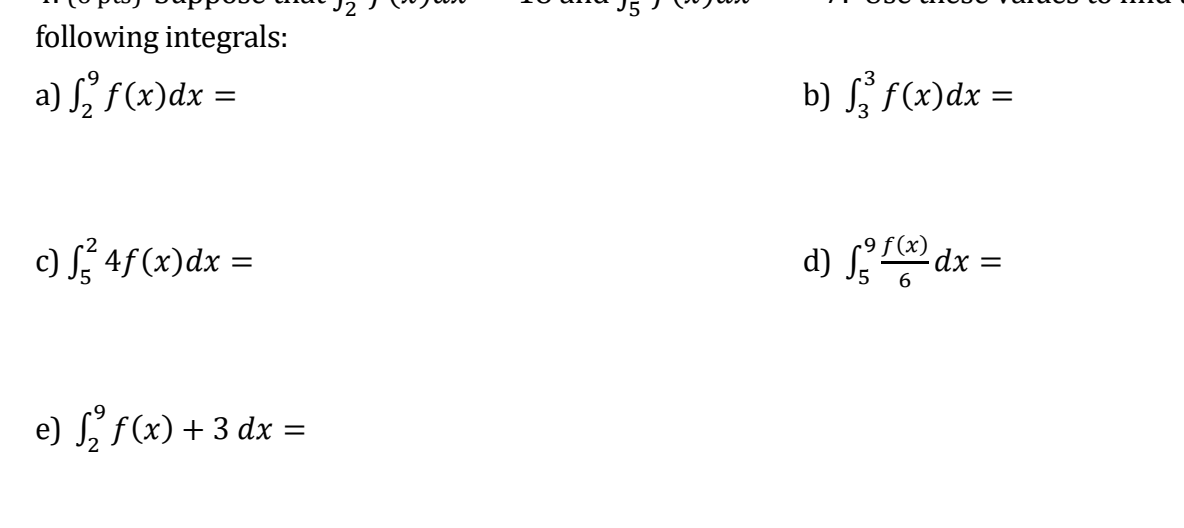

Find the exact area between the graph of e* + 12x and the x-axis on the interval [1,4]. | Let f(x) = %x'* %xz. Given that the derivative is f (x) = x3 9x, then the numbers for f(x) are -3, 0 and 3. Use that to answer the questions below: - (a) What are the x interval(s) where f(x) is increasing? And what are the x interval(s) where f(x) is decreasing? How do you know? (b) What are the x value(s) where f(x) has alocal minimum? And what are the x value(s) where f(x) has a local maximum? How do you know? 4 V = -mrs. The radius is growing at a rate3 of 5 cm/s. What is the rate of change of the volume when the radius is 6cm?Suppose that S, f(x)dx = 18 and f, f(x)dx = -7. Use these values to find the\fa) You want to construct an open box by b) Two numbers x and y must have a cutting square corners from a 10-inch by sum equal to 20, and we also require that 15-inch piece of rectangular cardboard the number x be at least 2 and at most 18. and folding up the sides. What size What is the largest possible value of the should you make the square corners in product function P = 2xy? And what is order to maximize the volume of the box? the smallest possible value of the product function P = 2xy
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


