1. Finding a small coloring

Let G be a graph of n vertices with chromatic number (G). Suppose that you cannot directly access G. Fortunately, you can access G via an oracle that behaves as follows. On the rst call to the oracle, the oracle returns a maximum independent set of G (in the form of a list of vertices) and then deletes from G the vertices in this set. On the second call to the oracle, the oracle returns the largest independent set in the remaining graph and then deletes these vertices from the graph as well. This process continues upon each successive call to the oracle. If you only wish to color n/2 vertices, what is the maximum number of times you must call the oracle in the worst case. Explain why this is the maximum number of calls needed.I need your help with this.

2. Listing vertices of a negative cycle

You are given a connected weighted graph G = (V,E). Describe an ecient algorithm that detects whether there is a negative cycle and, if there is a negative cycle, lists the vertices in the cycle. Be sure to explain why the algorithm is correct. Hint: Start with the Bellman-Ford algorithm.

3. Dijkstras algorithm and negative edge-weights

Explain what part Dijkstra's algorithm proof breaks when edge-weights can be negative.

4. Eulerian circuits

A graph is an even graph if every vertex has even degree. Prove that every even graph decomposes into cycles. That is, the edges of the graph can be partitioned into sets, and each set corresponds to the edges of a cycle of G. Note that the graph is not necessarily simple, so it can have multiple edges and loops.

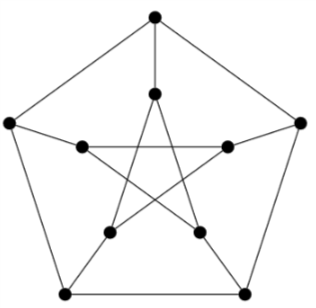
5. Graph coloring

(a) Let G be a graph with 5 (non-empty) independent sets, V1,V2,...,V5. Suppose that the subgraph induced by taking the vertices of any pair (Vi,Vj) of the independent sets is a complete bipartite graph. What is the chromatic number of G?

(b) Is the graph below 2-colorable? If so, show a proper 2-coloring. If not, explain why not, and show a proper k-coloring for the smallest possible value of k.