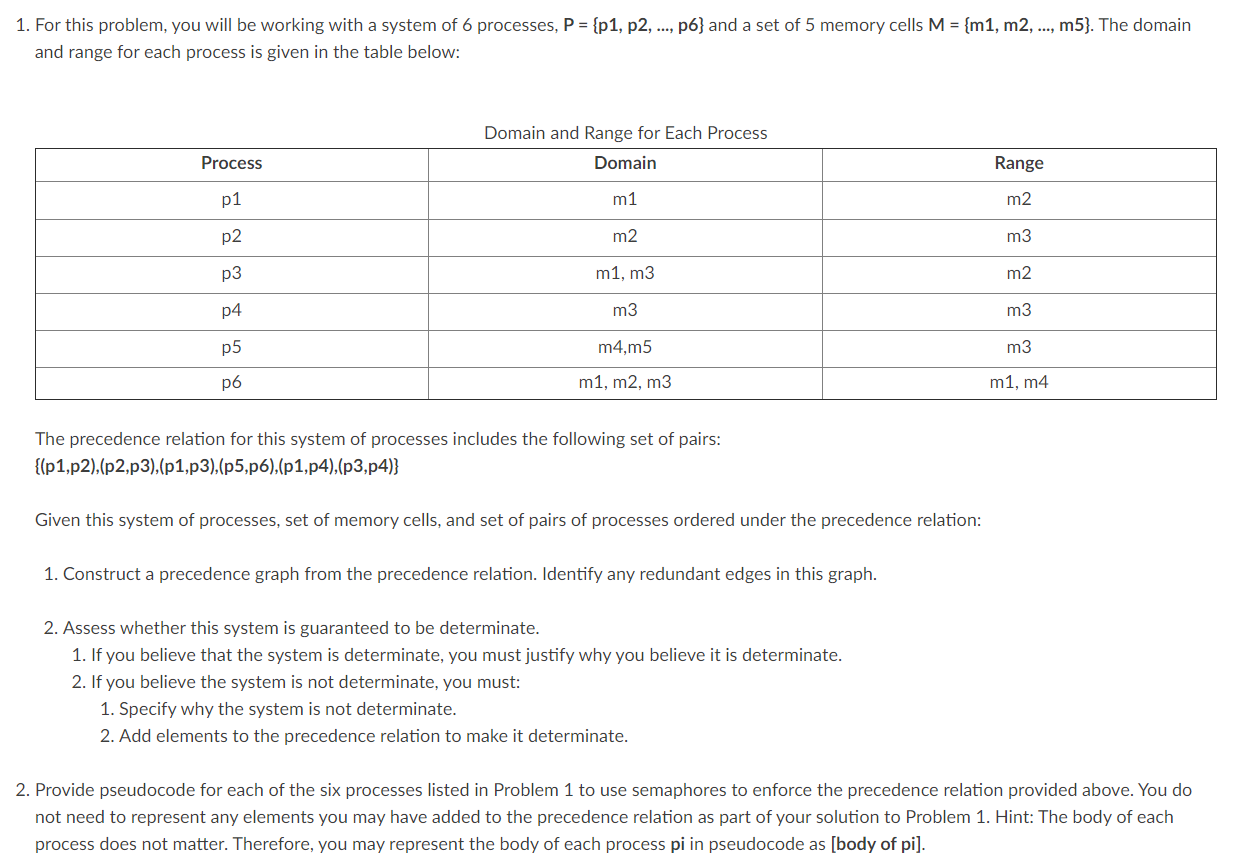
1. For this problem, you will be working with a system of 6 processes, P = {p1, p2, ..., p6} and a set of 5 memory cells M = {m1, m2, ..., m5). The domain and range for each process is given in the table below: Domain and Range for Each Process Domain Process Range p1 m1 m2 p2 m2 m3 p3 m1, m3 m2 p4 m3 m3 p5 m4,m5 m3 p6 m1, m2, m3 m1, m4 The precedence relation for this system of processes includes the following set of pairs: {{p1,p2),(p2,p3),(p1,p3),(p5,p6),(p1,p4),(p3,p4)} Given this system of processes, set of memory cells, and set of pairs of processes ordered under the precedence relation: 1. Construct a precedence graph from the precedence relation. Identify any redundant edges in this graph. 2. Assess whether this system is guaranteed to be determinate. 1. If you believe that the system is determinate, you must justify why you believe it is determinate. 2. If you believe the system is not determinate, you must: 1. Specify why the system is not determinate. 2. Add elements to the precedence relation to make it determinate. 2. Provide pseudocode for each of the six processes listed in Problem 1 to use semaphores to enforce the precedence relation provided above. You do not need to represent any elements you may have added to the precedence relation as part of your solution to Problem 1. Hint: The body of each process does not matter. Therefore, you may represent the body of each process pi in pseudocode as [body of pi). 1. For this problem, you will be working with a system of 6 processes, P = {p1, p2, ..., p6} and a set of 5 memory cells M = {m1, m2, ..., m5). The domain and range for each process is given in the table below: Domain and Range for Each Process Domain Process Range p1 m1 m2 p2 m2 m3 p3 m1, m3 m2 p4 m3 m3 p5 m4,m5 m3 p6 m1, m2, m3 m1, m4 The precedence relation for this system of processes includes the following set of pairs: {{p1,p2),(p2,p3),(p1,p3),(p5,p6),(p1,p4),(p3,p4)} Given this system of processes, set of memory cells, and set of pairs of processes ordered under the precedence relation: 1. Construct a precedence graph from the precedence relation. Identify any redundant edges in this graph. 2. Assess whether this system is guaranteed to be determinate. 1. If you believe that the system is determinate, you must justify why you believe it is determinate. 2. If you believe the system is not determinate, you must: 1. Specify why the system is not determinate. 2. Add elements to the precedence relation to make it determinate. 2. Provide pseudocode for each of the six processes listed in Problem 1 to use semaphores to enforce the precedence relation provided above. You do not need to represent any elements you may have added to the precedence relation as part of your solution to Problem 1. Hint: The body of each process does not matter. Therefore, you may represent the body of each process pi in pseudocode as [body of pi)