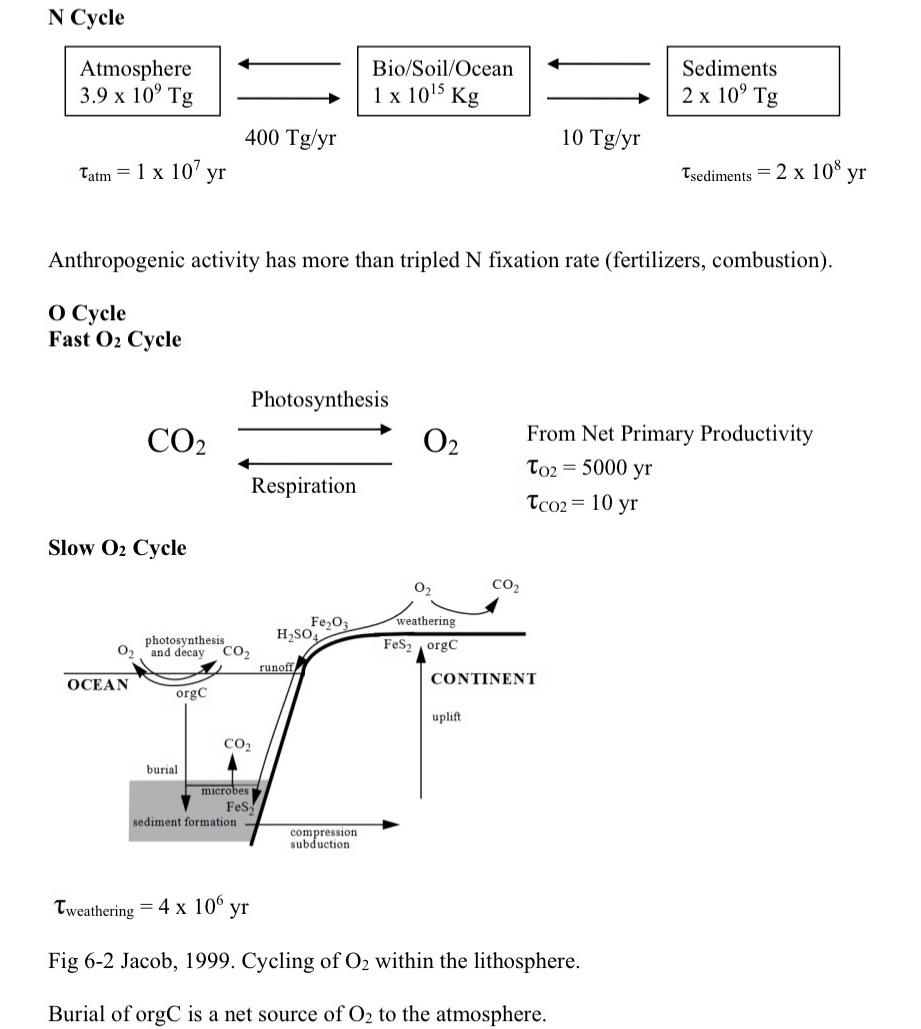
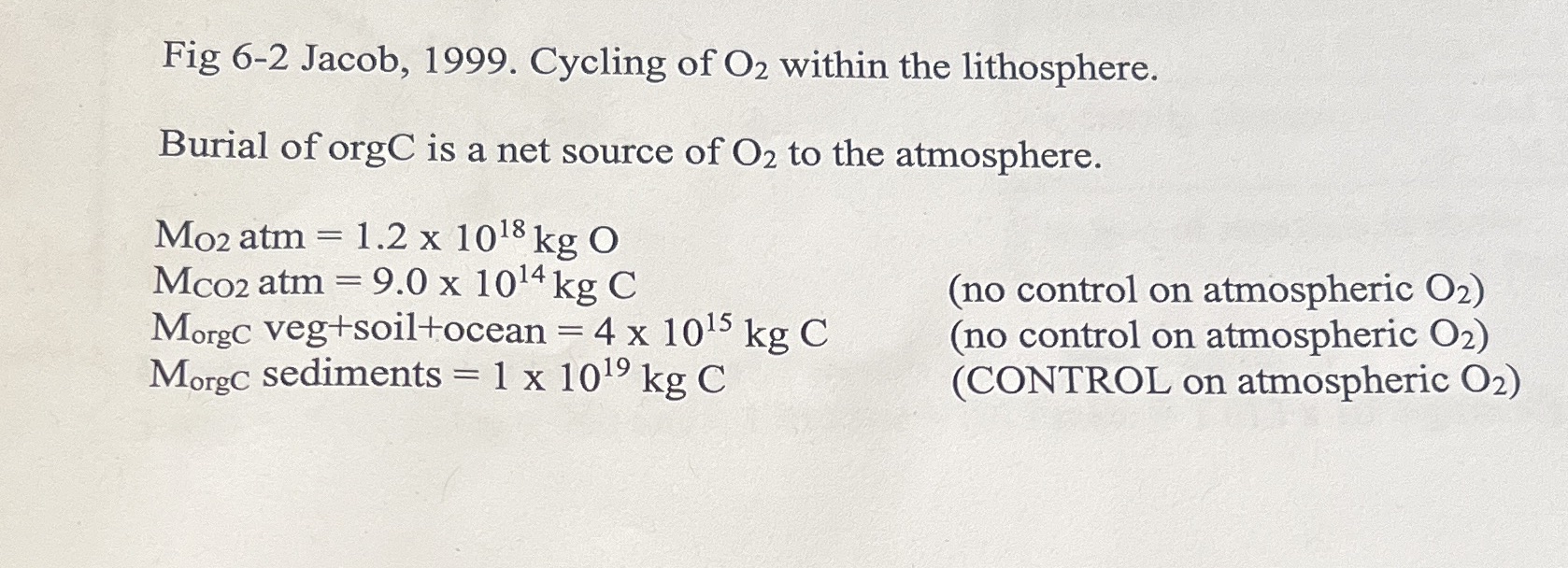
#

1) Geochemical Box Models Consider an element X exchanging between two geochemical reservoirs A and B. Let MA and MB be the masses of X in reservoirs A and B, respectively; let TA and B be the residence times of X in reservoirs A and B, respectively. Further let MT= MA + MB be the total mass of X in the two reservoirs combined. i) (15 PTS) Derive the steady state relationship: MA MT = 1+- TB ii) (10 PTS) In the limit TA >> TB, what controls the value of MA? iii) (20 PTS) Consider a situation where additional mass M' is injected into reservoir A at time t=0 increasing the total amount of element X in the system from Mo to M1, with no further injection at later times; further assume that TA >> TB, that the total mass in the altered system is M = Mo + M', and that Mo < < M'. Give an expression for MB(t) as a function of M1, TA, TB, and t. (Hint: start with an expression of dMB/dt and later integrate to get MB(t)) What is the characteristic time for MB to approach steady state? What is the characteristic time for MA to approach steady state?