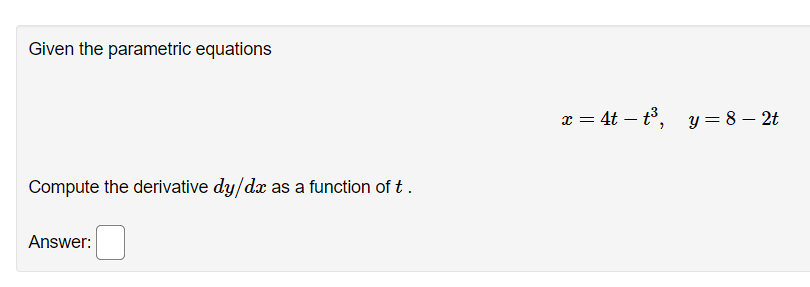
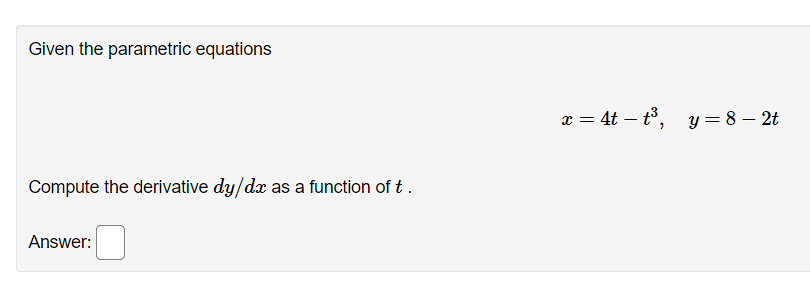
Question: 1. Given the parametric equations x =4t - +3, y =8 - 2t Compute the derivative dy/ da as a function of t . Answer:Find








1.

![one write them as a comma separated list, e.g. (1,2):(3,4)) C]. At](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6664590ba6d84_4276664590b94d6b.jpg)
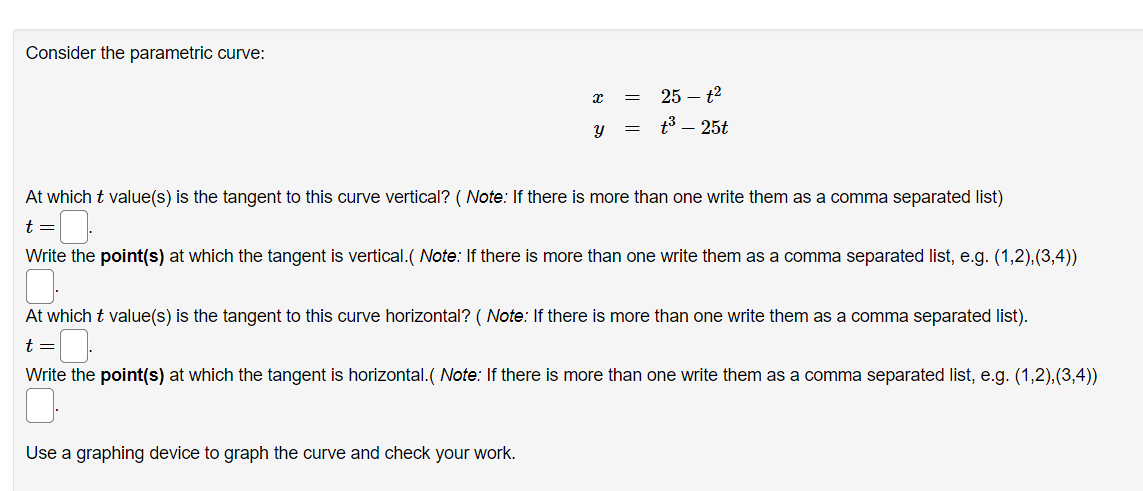
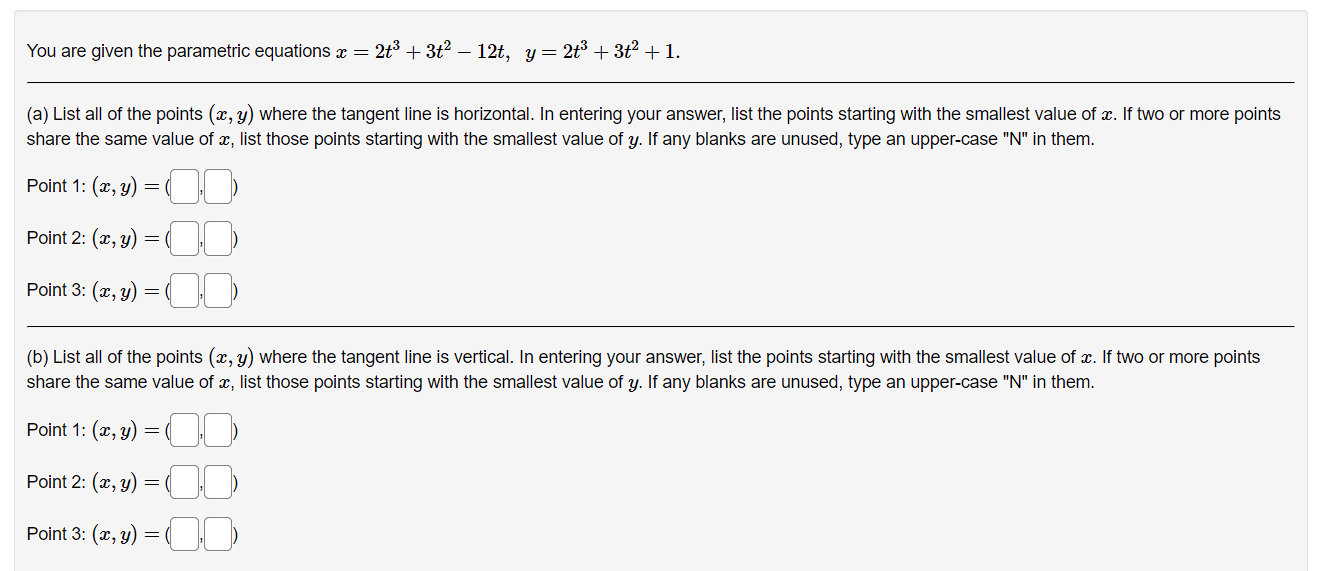






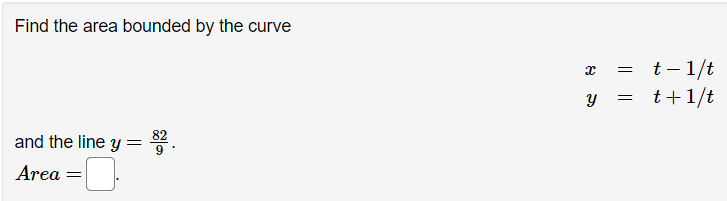
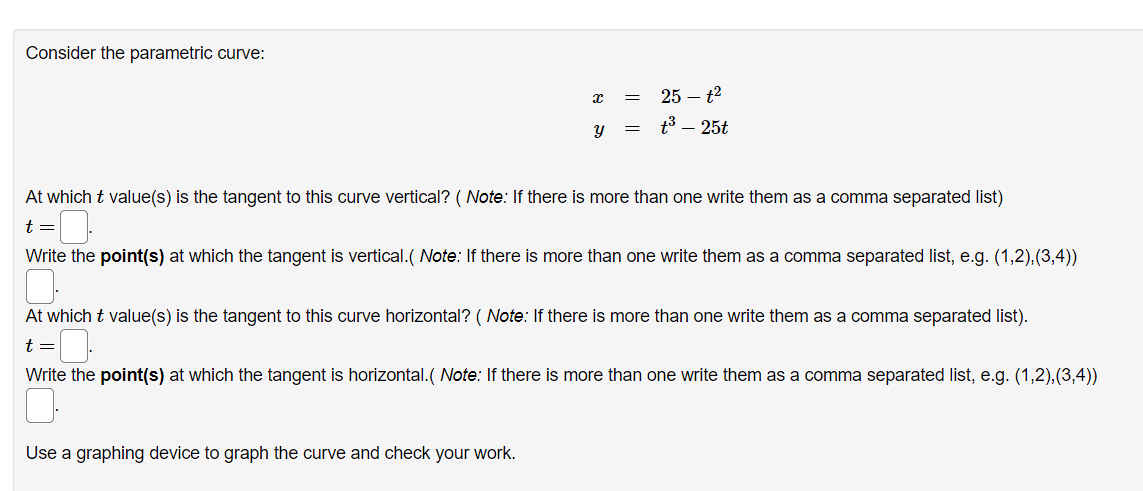
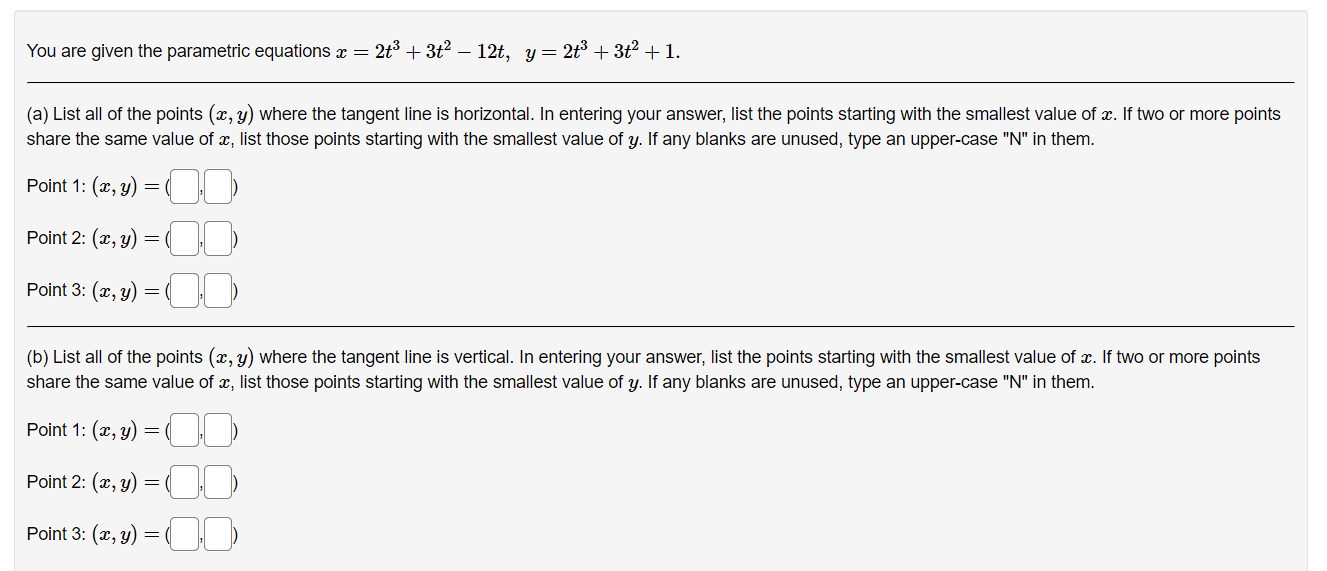
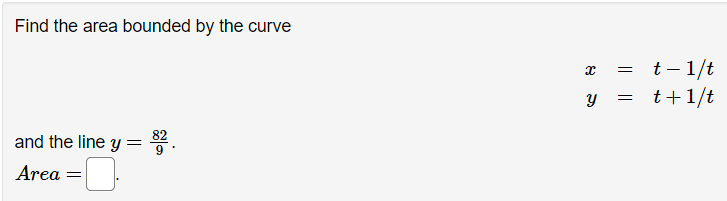
Given the parametric equations x =4t - +3, y =8 - 2t Compute the derivative dy/ da as a function of t . Answer:Find the equation for the line tangent to the parametric curve: 13 - 9t = 9t2 - 14 at the points where t = 3 and t = -3. For t = 3, the tangent line (in form y = max + b) is y = Fort = -3 , the tangent line is y =(a) Find dy expressed as a function of t for the given the parametric equations: a: :1: = Qtihlt y = Altht 03 ac (b) Find dE expressed as a function of t. a: d2 a- Consider the parametric curve: 3 = 25t2 y = t325t At which if value(s) is the tangent to this curve vertical? ( Note: If there is more than one write them as a comma separated list) 1:28. Write the point{s} at which the tangent is vertical.( Note: If there is more than one write them as a comma separated list, e.g. (1,2):(3,4)) C]. At which if value(s) is the tangent to this curve horizontal? (Note: if there is more than one write them as a comma separated list). 1:28. Write the point{s} at which the tangent is horizontal.( Note: lfthere is more than one write them as a comma separated list. e.g. (1:2),(3:4)) Use a graphing device to graph the curve and check your work. You are given the parametric equations a: = 2:3 + 3:2 i 12$, 3; 2 2t3 + 3i:2 + 1. (a) List all of the points (at, y) where the tangent line is horizontal. In entering your answer, list the points starting with the smallest value of as. If two or more points share the same value 013:, list those points starting with the smallest value of y. If any blanks are unused, type an upper-case "N\" in them. Point]: (3, y] = (D'D) Point2: (2:, y) = (D.D) PointS: (1,3,!) = (D'D) (b) List all of the points (ac, y) where the tangent line is vertical. In entering your answer, list the points starting with the smallest value 013:. If two or more points share the same value 012:, list those points starting with the smallest value of Q. If any blanks are unused, type an upper-case "N\" in them. Point 1: (x, y] = DD) Point2: (x, y] = (D'D) Point3: (1:, y) : (D.D) Use a graph to estimate the coordinates of the highest point and the leftmost point on the curve a: = tet, y = tst. Then find the exact coordinates. Highest point: Leftmost point: The curve has one horizontal asymptote and one vertical asymptote. Find them. Horizontal asymptote: y 2 Vertical asymptote: :c = Which of the following integrals represents the length of the parametric curve x = t + cos(t), y = t - sin(t), 0
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


