1. If the objective function coefficient of T3 increases by $50, will the optimal solution change? What about the value of the objective function?

2. How much should the objective function coefficient of T4 decrease for that to become an attractive alternative?

3. We can decrease C requirement by 3 units, while increasing the A requirement by 0.25 units. Is it worth the effort?

4. If the objective function coefficient of T1 decreases by $40 and the objective function coefficient of T2 increases by $10, what will be the impact on cost?

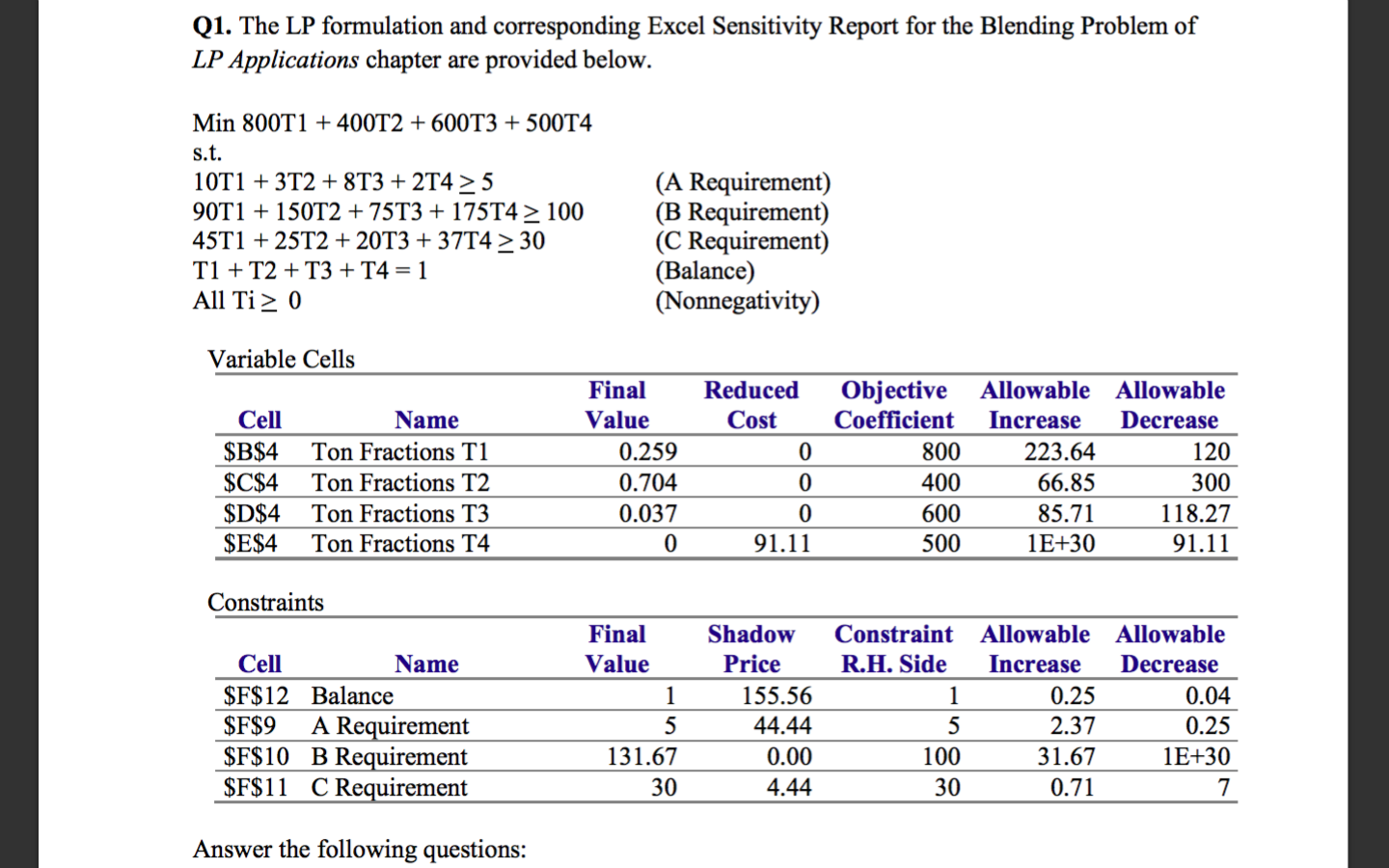
Q1. The LP formulation and corresponding Excel Sensitivity Report for the Blending Problem of LP Applications chapter are provided below. Min 800T1 + 400T2 + 600T3 + 500T4 s.t. 10T1 + 3T2 + 8T3 + 2T4 >5 90T1 + 150T2 + 75T3 + 17514 > 100 45T1 + 25T2 + 2013 + 3714 > 30 T1 + T2 + T3 + 14 = 1 All Ti> 0 (A Requirement) (B Requirement) (C Requirement) (Balance) (Nonnegativity) Variable Cells Reduced Cost Cell $B$4 $C$4 $D$4 $E$4 Name Ton Fractions T1 Ton Fractions T2 Ton Fractions T3 Ton Fractions T4 Final Value 0.259 0.704 0.037 0 Objective Coefficient 800 400 600 500 Allowable Allowable Increase Decrease 223.64 120 66.85 300 85.71 118.27 1 E+30 91.11 0 0 91.11 Constraints Cell Name $F$12 Balance $F$9 A Requirement $F$10 B Requirement $F$11 C Requirement Final Value 1 5 131.67 30 Shadow Price 155.56 44.44 0.00 4.44 Constraint Allowable Allowable R.H. Side Increase Decrease 1 0.25 0.04 5 2.37 0.25 100 31.67 1E+30 30 0. 71 7 Answer the following questions