1 ) Is it possible to have a relation on the set {a, b, c} that is both symmetric and anti-symmetric? If so, give an example.

2)

For each relation R, indicate if the relation is

• Reflexive, anti-reflexive, or neither
• Symmetric, anti-symmetric, or neither
• Transitive or not transitive

The domain of the relation R is {a, b}. R = {(a, b), (b, a), (a, a), (b, b)}

3 )

X = {a, b, c, d, e}, and P(X) is the power set of X. The domain of all of the relations defined below is P(X).

For each relation, indicate if the relation is

• Reflexive, anti-reflexive, or neither
• Symmetric, anti-symmetric, or neither
• Transitive or not transitive
• only b ,c please :)
• 

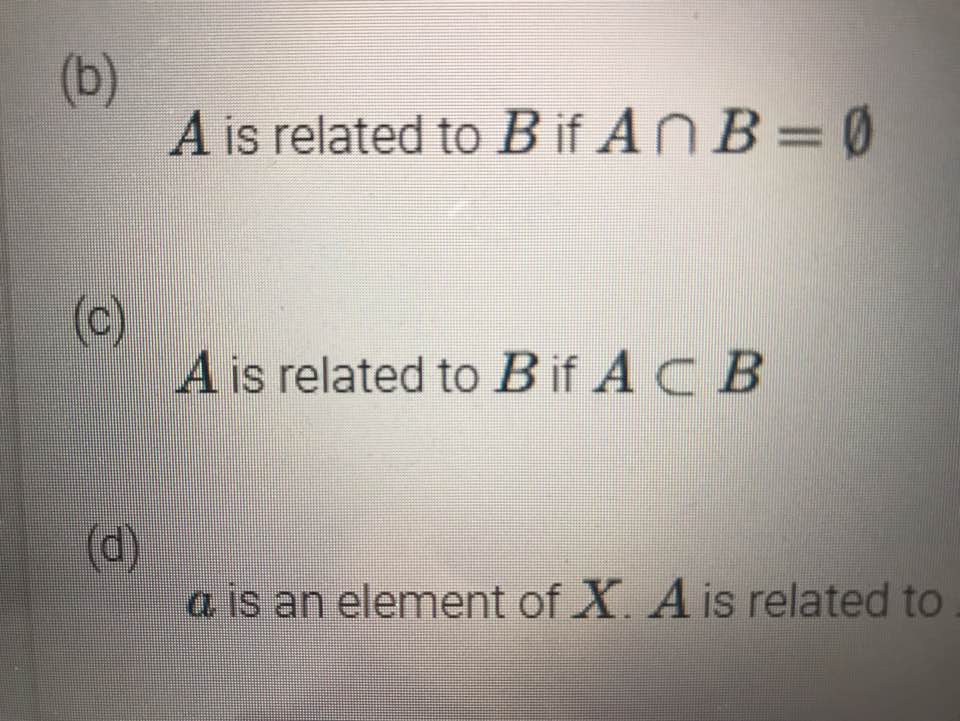
(b) A is related to B if An B=0 (c) A is related to B if ACB a is an element of X. A is related to