Question: 6. Let A = {x E Z |x 2 5a + 2 for some integer a}, B = {y E Z | y = 10!)



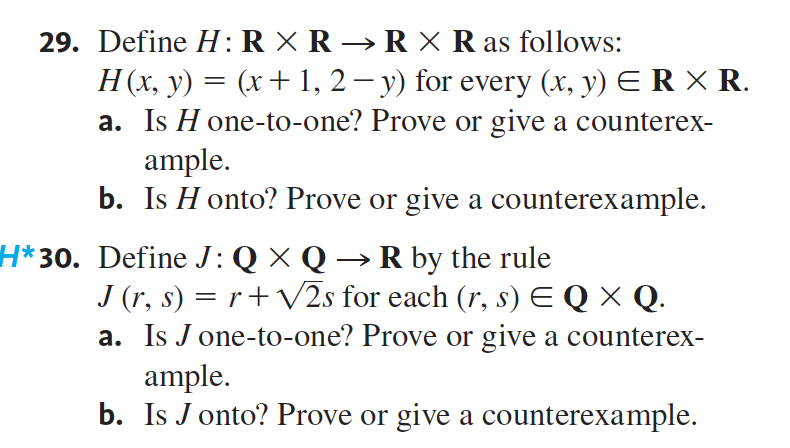






![= 4k, for some integer k} A] = {n E Z I](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6703ec210c0ac_3046703ec20b6099.jpg)


6. Let A = {x E Z |x 2 5a + 2 for some integer a}, B = {y E Z | y = 10!) 3 for some integer b}, and C = {z E Z | z = 106 + 7 for some integer C}. Prove or disprove each of the following statements. a.AB b.BA HoBzC 7. Let A = {x E Z lx = 601 + 4 for some integera}, B = {y E Z | y = 182) 2 for some integer b}, and C = {z e Z | z = 186 +16 for some integer c}. Prove or disprove each of the following statements. a.AB b.BA c.B=C \f30. Let Z be the set of all integers and let 31. A0 = {n E Z I n = 4k, for some integer k} A] = {n E Z I n = 4k+ 1, for some integer k} A2 = {n E Z I n = 4k+ 2, for some integer k} and A3 = {n E Z I n = 4k+ 3, for some integer k}. Is {A0,A1, 142,143} a partition of Z? Explain your answer. Suppose A = {1,2} andB = {2, 3}. Find each of the following: a. @(A D B) b. @(A) c. @(A U B) d. @(A X B) 13. Let 15 = {0, l, 2, 3, 4}, and define functions f: J5 ) J5 and g: 15 ) J5 as follows: For each XEJj, f (x) = (x + 4)2 mod 5 and 30c) = (x2 + 3x+ 1) mod 5. Is f= 3? Explain. 29. Define H: R X R > R X R as follows: H(x,y) = (x+1,2y)forevery(x,y) E R X R. a. 13 H onetoone? Prove or give a counterex ample. b. Is H onto? Prove or give a counterexample. H*30. Define J: Q X Q ) R by the rule J(r, S) = r+\\725 foreach (r, S) E Q X Q. a. Is J onetoone? Prove or give a counterex ample. b. Is I onto? Prove or give a counterexample. 20. Define Floor: R > Z by the formula Floor(.r) = [x], for every real number x. a. Is Floor one-to-one'? Prove or give a counterexample. b. Is Floor onto? Prove or give a counterexample. 21. Let S be the set of all strings of 0's and 1's, and define L: S > Znomeg by L(s) = the length of s, for every string 5 in S. a. Is L onetoone? Prove or give a counterex ample. b. Is L onto? Prove or give a counterexample. In each of 15-18 a function f is defined on a set of real numbers. Determine whether or not fis one-to-one and justify your answer. xtl 15. f (x) = for each number x * 0 X 16. f(x) = for each real number x 7-2 + 1 3x - 1 17. f(x) = for each real number x # 0 X x+1 18. f(x) = for each real number x * 1 x-1Exercises 36 and 37 use the following definition: If f: R > R and g: R ) R are functions, then the function (f+ g): R > R is defined by the formula (f+g)(x) = f(x) + g(x) for every real number x. 36. Iff: R > R and g: R > R are both onetoone, is f + g also onetoone? Justify your answer. 37.1ff:R > Randg1R > Rare both onto, is f+g also onto? Justify your answer. Exercises 38 and 39 use the following definition: if f: R > R is a function and c is a nonzero real number, the function (c-f): R ) R is defined by the formula (c-f)(x) = C(f(x)) for every real number x. 38. Letf: R > R be a function and c a nonzero real number. If f is onetoone, is c- f also onetoone? Justify your answer. 39. Let f: R > R be a function and c a nonzero real number. If f is onto, is c- f also onto? Justify your answer. Draw the directed graphs of the relations defined in 13-18. 13. Define a relation R on A = {0, 1, 2, 3} by R = { (0, 0), (1, 2), (2, 2) }. 14. Define a relation S on B = {a, b, c, d} by S = {(a, b), (a, c), (b, c), (d, d)}. 15. Let A = (2, 3, 4, 5, 6, 7, 8) and define a relation R on A as follows: For every x, y E A, x Ry 4 x y. H 16. Let A = {5, 6, 7, 8, 9, 10} and define a relation S on A as follows: For every x, y E A, xSy + 2 ( x-y). 17. Let A = {2, 3, 4, 5, 6, 7, 8} and define a relation T on A as follows: For every x, y E A, xTy + 3 ( x- y). 18. Let A = {0, 1, 3, 4, 5, 6} and define a relation V on A as follows: For every x, y E A, x Vy + : 5/ ( 12 - 12 ).In 933, determine whether the given relation is reflexive, symmetric, transitive, or none of these. justify your answers. 9. R is the \"greater than or equal to\" relation on the set of real numbers: For every x, y E R, x R y #1 x 2 y. 10. C is the circle relation on the set of real numbers: Foreveryx,y E R,ny4:rx2+y2 =1. 11. D is the relation defined on R as follows: For everyx,y E R,ny<: a in each of the relation r is an equivalence on set a. find distinct classes r. b c d ... defined as follows: for all x y ea xry ry determine whether given reflexive sym- metric transitive or none these. justify your answers. than equal to real numbers: er h zy. circle cy x2 y2="1." dy xy e congruence modulo z: m n ez en f> 51(m -n). 14. O is the relation defined on Z as follows: For all m, n E Z, m On m - n is odd. 15. D is the "divides" relation on Z+: For all positive integers m and n, m Dn min. 16. A is the "absolute value" relation on R: For all real num- bers x and y, x Ay + Ixl = lyl.24. A sequence a1, a2, a3, .. . is defined by letting al = 3 and ak = 7ak_1 for all integers k 2 2. Show that an = 3. 7-1 for all integers n > 1. 25. A sequence bo, bj, b2, .. . is defined by letting bo = 5 and bk = 4 + bk-1 for all integers k > 1. Show that by > 4n for all integers n 2 0
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


