Question: 1. Let A = 1 3 4 3 2 6 5 1 8 and b = b1 b2 b3 . (a) Show that the matrix

1. Let A = 1 3 4 3 2 6 5 1 8 and b = b1 b2 b3 . (a) Show that the matrix Ax = b does not have a solution for all possible b; that is, show that there exists at least one b for which Ax = b does not have a solution. (b) Describe the set of all b for which Ax = b does have a solution.

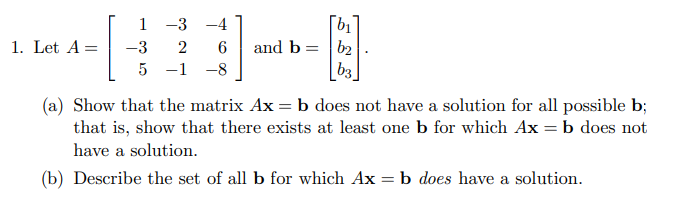
-4 b1 1. Let A = -3 2 6 and b = b2 5 -1 -8 b3 (a) Show that the matrix Ax = b does not have a solution for all possible b; that is, show that there exists at least one b for which Ax = b does not have a solution. (b) Describe the set of all b for which Ax = b does have a solution

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

Use MATLAB code to find the solution. Please only do e) and f) since they have been solved previous questions have been answered. Assume 1 8 3 5 0 6 -3 4 -2 2 2 -5 a) Find matrix B by adding a...

Write a C++ program that determines if a given N matrix is a magic square, where N Magic Square: An N Magic Square is a N matrix (i.e... a square N x N matrix) with positive integer values for its...

Consider the following file with "triangular" data, if you will. Run the next set of four cells to create the data files that will be needed in the test cases further below (data_1.datdata_4.dat). In...

Two weeks later, you are assigned to the Quant team and you are asked by the team leader to generate a SGD discount factor table for 5 years. The cost of borrowing has increased to 3% yet the cost of...

For EACH of the 6 data sets... Randomly (using a Vlookup or something similar to randomize) select a sample of 4 and add them together, repeat this 39 times so you have a total of 40 data points....

Intro The following table shows rates of return for a mutual fund and the market portfolio (S&P 500). A B C 1 Year Fund Market 1 14% 13% 2 -12% -14% 3 -6% -3% 4 5% 28% 6 5 14% 8% 7 6 7% 8% Part 1...

The following activities took place in March: Mar. 1(a) 1(c) 1(d) Purchased children laptop toys from Esorbma Limited, $94,000, terms 1/10, n/30, FOB shipping point. (b)The responsible party paid the...

Exercise 9-9 Writing off receivables LO P2 Daley Company estimates uncollectible accounts using the allowance method at December 31. It prepared the following aging of receivables analysis Days Past...

What formatting guidelines should be followed if a letter is too long to fit onto one page?

Use Excel to answer all of the following questions: #1. ABC company records during the past six weeks indicate the number of jobs requests: WEEK 1 2 3 4 5 6 Requests 45 38 36 42 46 43 Required:...

A new project will require an increase in net working capital. This increase in NWC will result in: ( Choose one )

4 12.5 points eBook A company reports the following for one of its products. Direct materials standard (3 pounds @ $2 per pound) Actual direct materials used (AQ) Actual units produced Actual cost of...