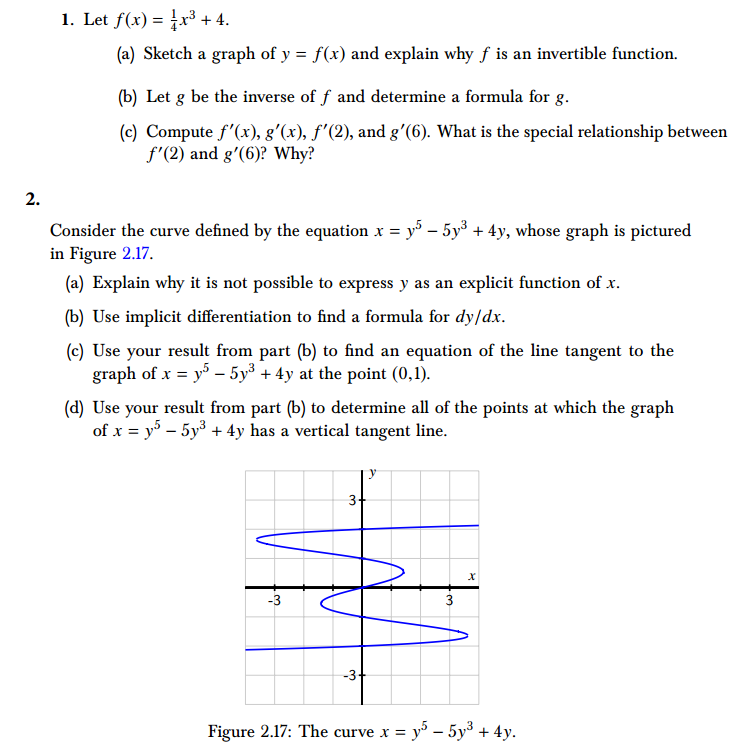
1. Let f(x) = x3 + 4. (a) Sketch a graph of y = f(x) and explain why f is an invertible function. (b) Let g be the inverse of f and determine a formula for g. (c) Compute f'(x), g'(x), f'(2), and g(6). What is the special relationship between f'(2) and g'(6)? Why? 2. Consider the curve defined by the equation x = y5 5y +4y, whose graph is pictured in Figure 2.17. (a) Explain why it is not possible to express y as an explicit function of x. (b) Use implicit differentiation to find a formula for dy/dx. (c) Use your result from part (b) to find an equation of the line tangent to the graph of x = y5-5y3 + 4y at the point (0,1). (d) Use your result from part (b) to determine all of the points at which the graph of xy55y3+ 4y has a vertical tangent line. -3 3- -3- 3 x Figure 2.17: The curve x = y5 - 5y3+4y.