1 of20

The least expected value in each contingency table cell in order for a chi-square test to be effective is...

	5
	4
	3
	2

2 of20

The null hypothesis for the chi-square goodness-of-fit test states that the distribution of

	cases for each group is equal to the expected distribution based on theory/knowledge of the population.
	cases for each group is not equal to the expected distribution based on theory/knowledge of the population.
	sample means is equal to expectation.
	sample means for each group is equal.

3 of20

The number of accidents in a factory for each month is provided:

Jan	Feb	Mar	Apr	May	June	July	Aug	Sep	Oct	Nov	Dec
25	28	24	18	17	27	9	18	22	14	12	26

Which hypothesis test would be appropriate for determining whether some months have a greater number of accidents than others?

	Least-squares regression
	Two-sample z-test for means
	Chi-square test for goodness of fit
	Chi-square test for independence
	One-sample z-test for means

4 of20

The degrees of freedom for a 2 x 2 contingency table for the chi-square test of independence equal

	4
	1
	2
	3

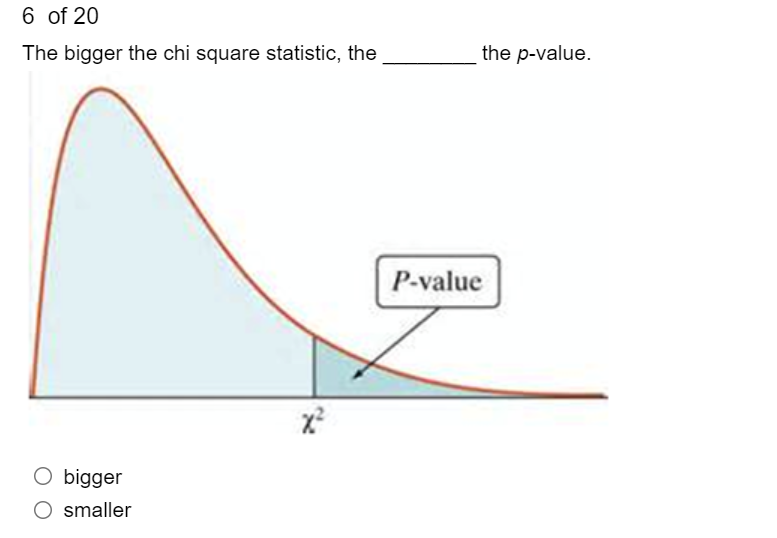
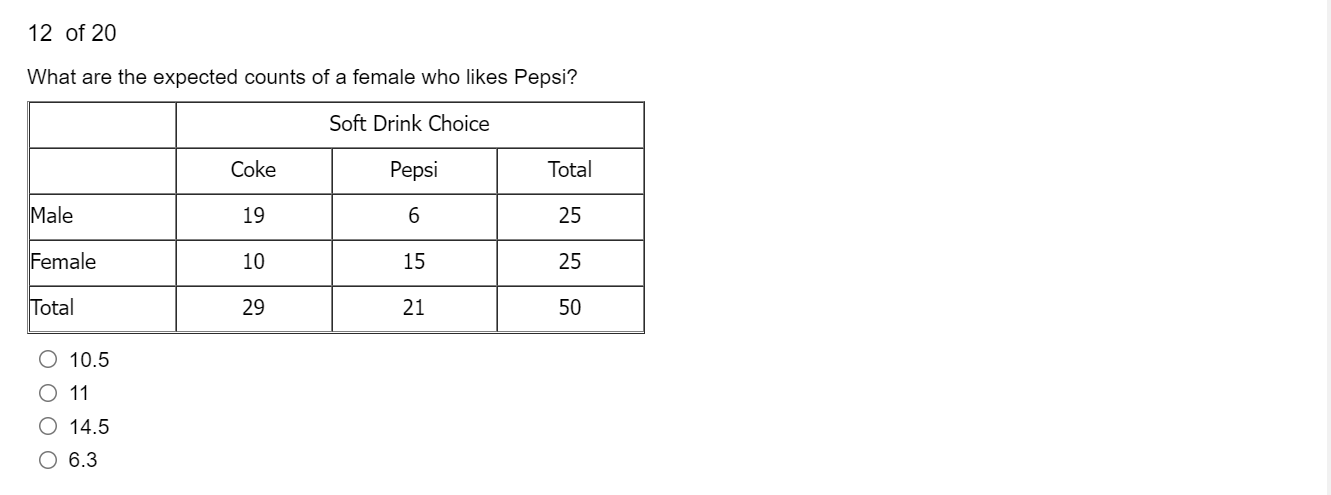
6 of 20 The bigger the chi square statistic, the the p-value. P-value O bigger O smaller9 of 20 Which of the following is the correct formula for the chi-square goodness-of-fit test? O EO - EE E O X E(0 - E) E O 2 = E (0 - E) O X' = [(0 - E) E\f5 of 20 When the expected values (E) are obtained by multiplying row totals by column totals and dividing by N E = x the chi-square test is N O equivalent to a one-sample t test. O a chi-square test of independence. O not valid. O a chi-square goodness-of-fit test