is typed as lambda, as alpha. Assume the PDE} (1 point) A is typed as lambda, a as alpha. Assume the PDE + m

λ is typed as lambda, α as alpha. Assume the PDE}

 

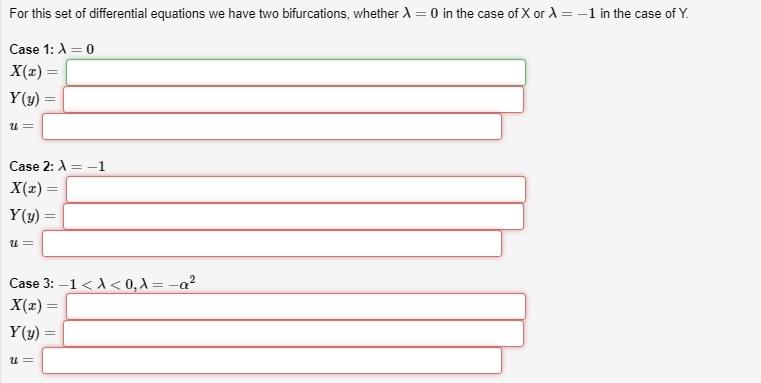
(1 point) A is typed as lambda, a as alpha. Assume the PDE + m dy? is separable by making the substitution u = XY: %3D Move the term with Y" to the right hand side and divide both sides by XY so that we get the separated ODE's: = -A Note: Use the prime notation for derivatives, so the derivative of X is written as X'. Do NOT use X'(x) Since these differential equations are independent of each other, they can be separated DE in X: DE in Y: Now we solve the separate separated ODES for the different cases in A. In each case the general solution in X is written with constants a and b and the general solution in Y is written with constants c and d. Write the functions alphabetically, so that if the solutions involve cos and sin, your answer would be acos(x) + bsin(x).