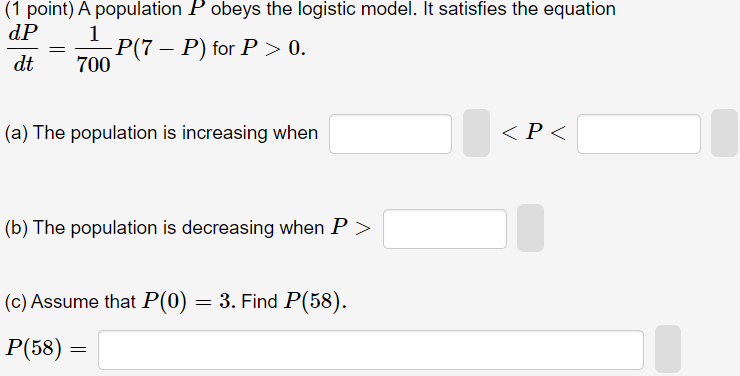
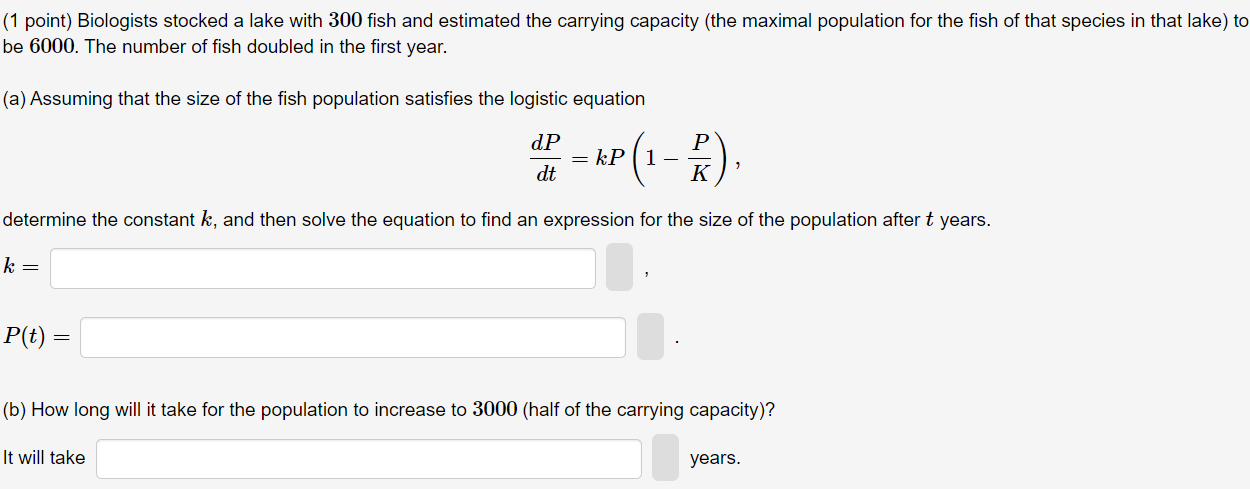
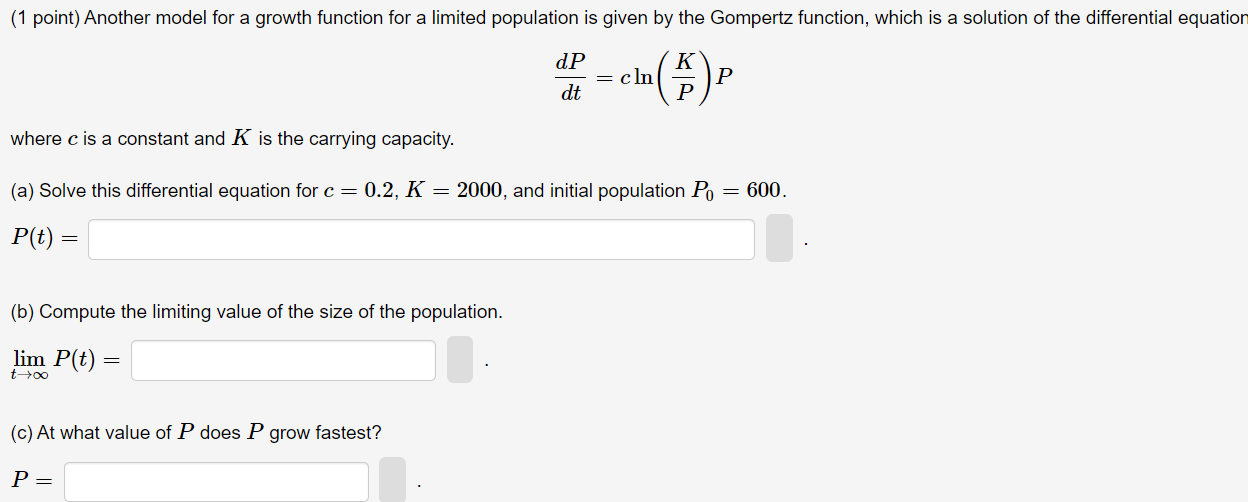
(1 point) A population P obeys the logistic model. It satises the equation JP 1 =P7P f Prat}. at 700 l l W (a) The population is increasing when 4:: P s\": (b) The population is decreasing when P 2:, [c] Assume that 13(0) 2 3. Find P(58). 12153) = (1 point) Biologists stocked a lake with 300 fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake) to be 6000. The number of fish doubled in the first year. (a) Assuming that the size of the fish population satisfies the logistic equation dp = KP (1 - P dt K determine the constant k, and then solve the equation to find an expression for the size of the population after t years. k = P(t) = (b) How long will it take for the population to increase to 3000 (half of the carrying capacity)? It will take years.(1 point) Another model for a growth function for a limited population is given by the Gompertz lunction, which is a solution of the differential equation dP K where c is a constant and K is the canying capacity. (a) Solve this differential equation for c = 0.2. K = 2000, and initial population P0 = 600. P[t) = (b) Compute the limiting value of the size of the population. ljm P(t) : tmo (c) At what value of P does P grow fastest? P