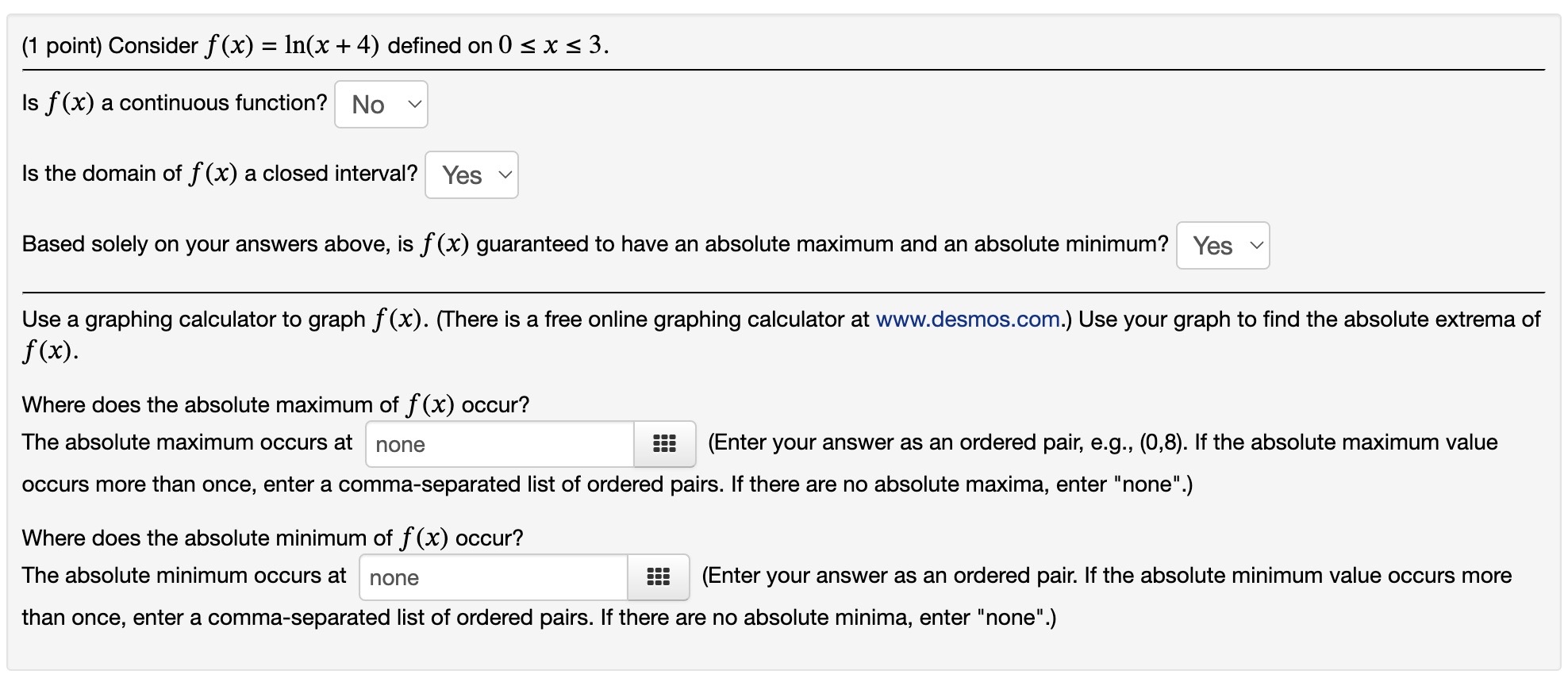
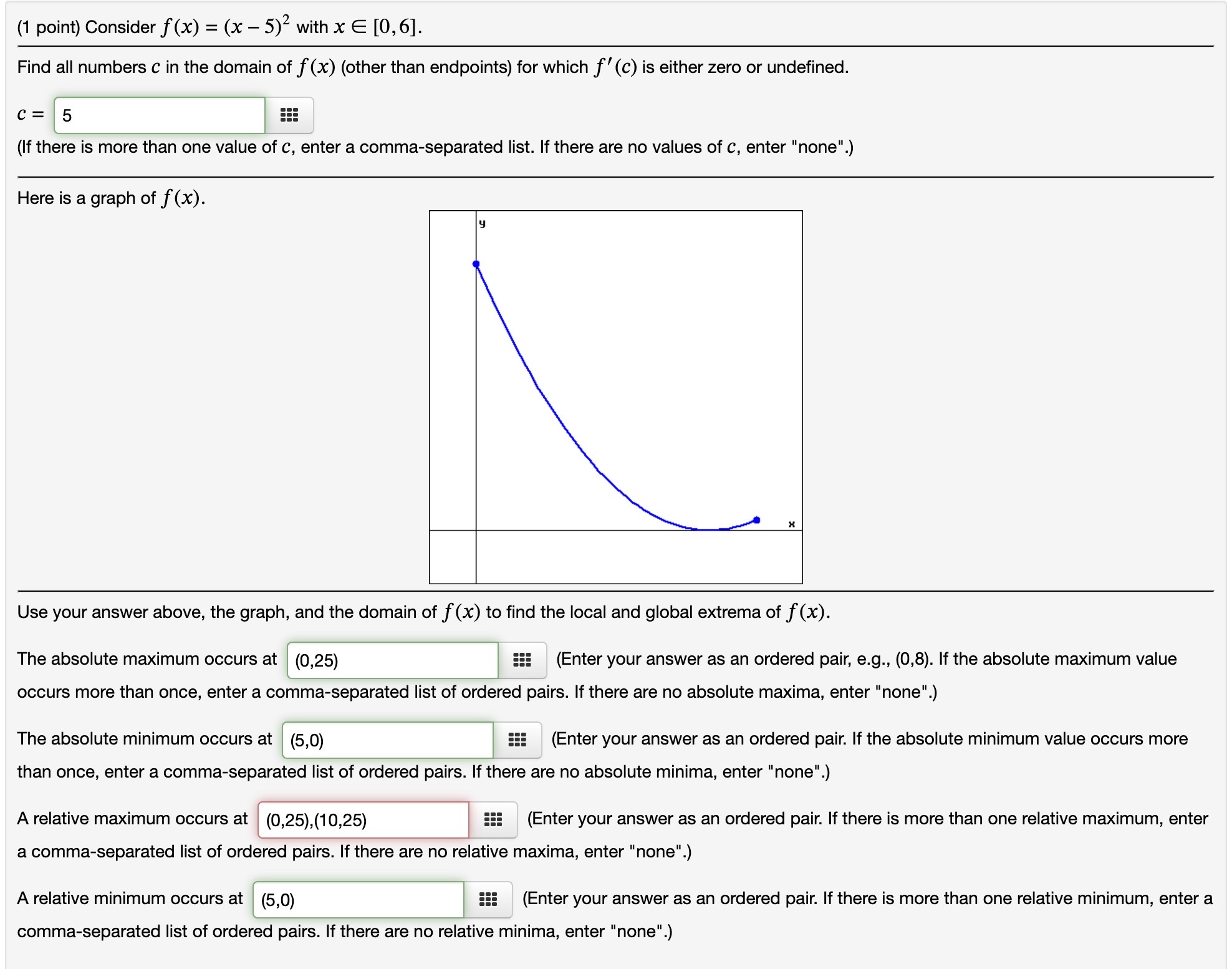
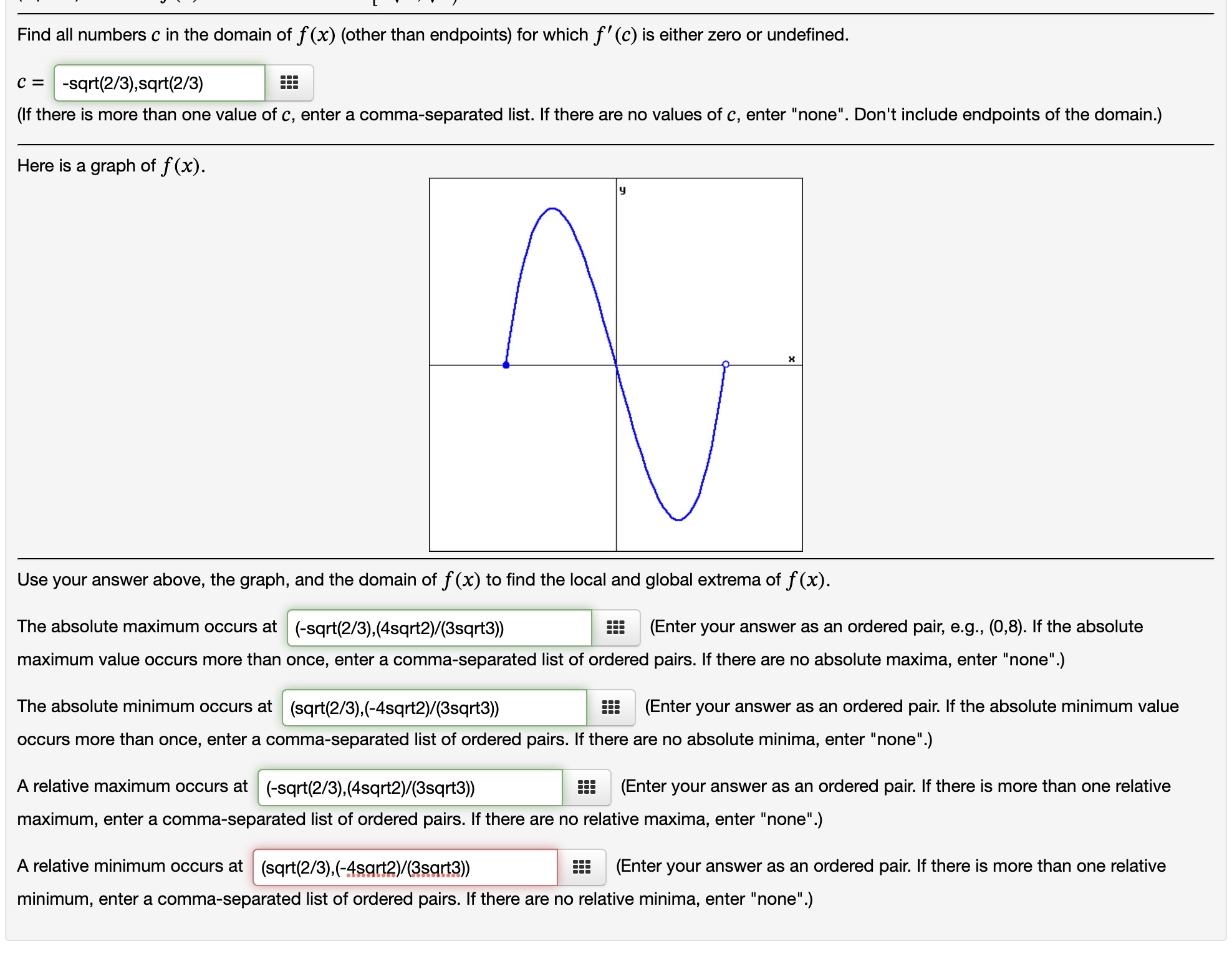
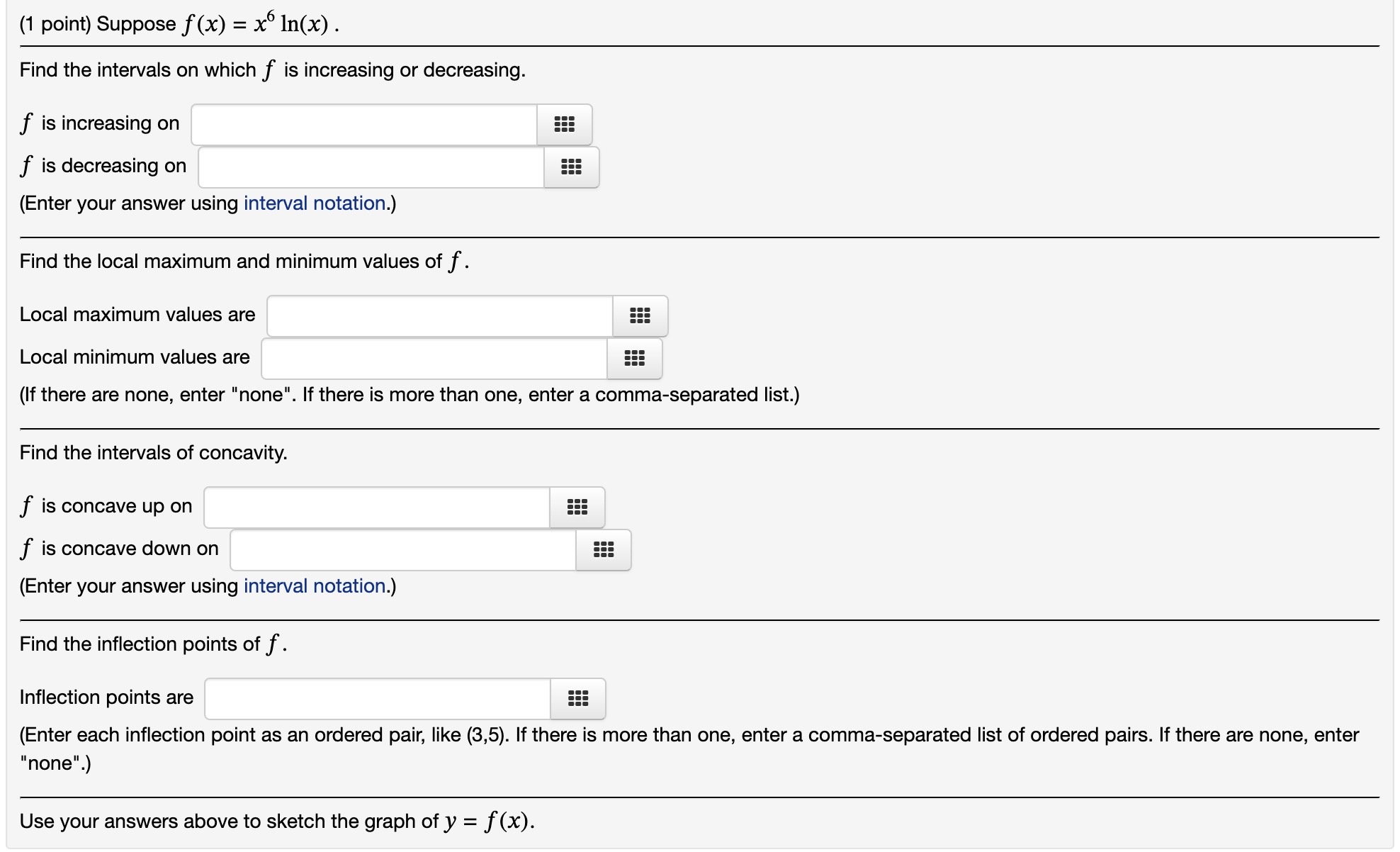
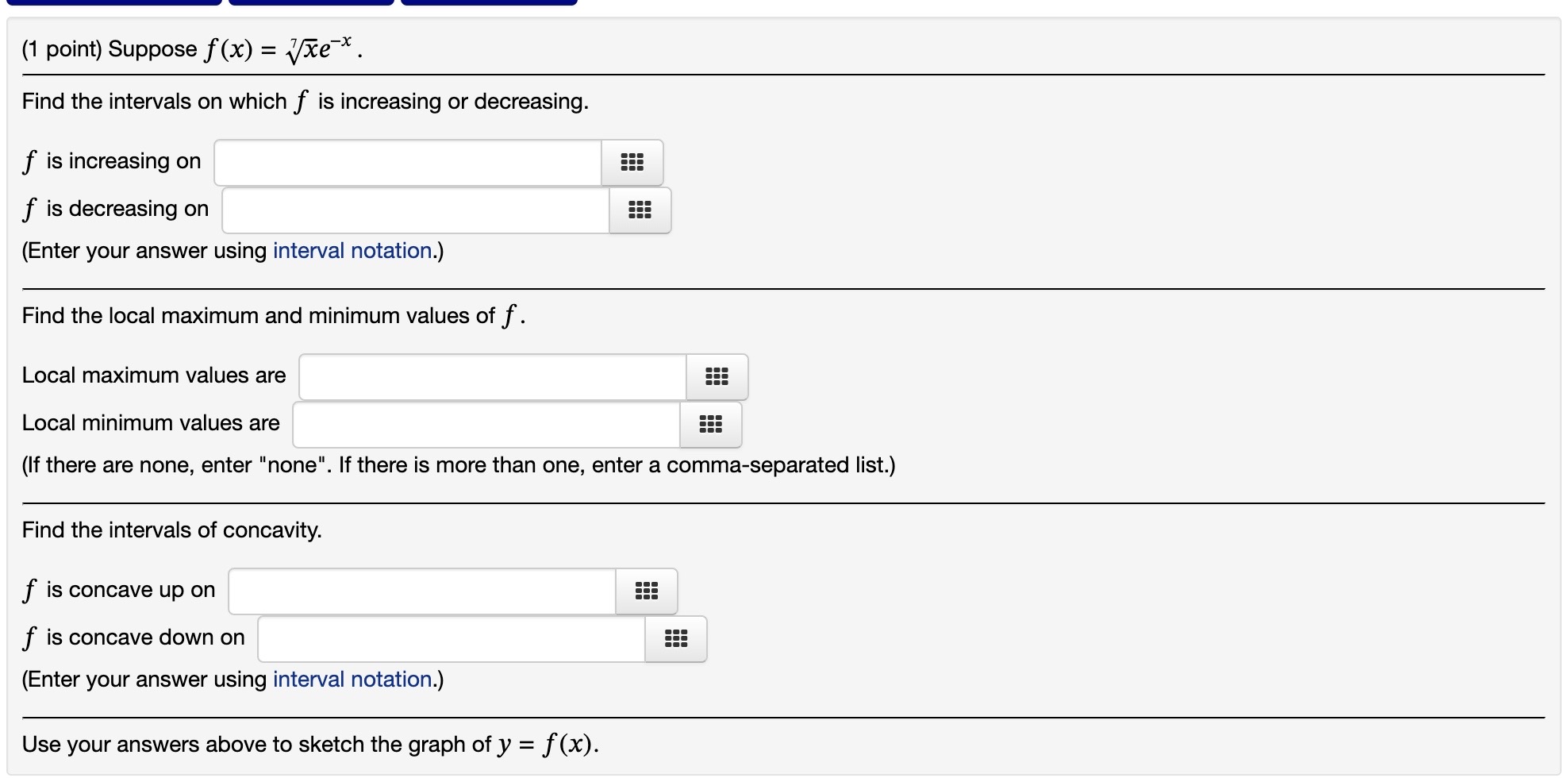
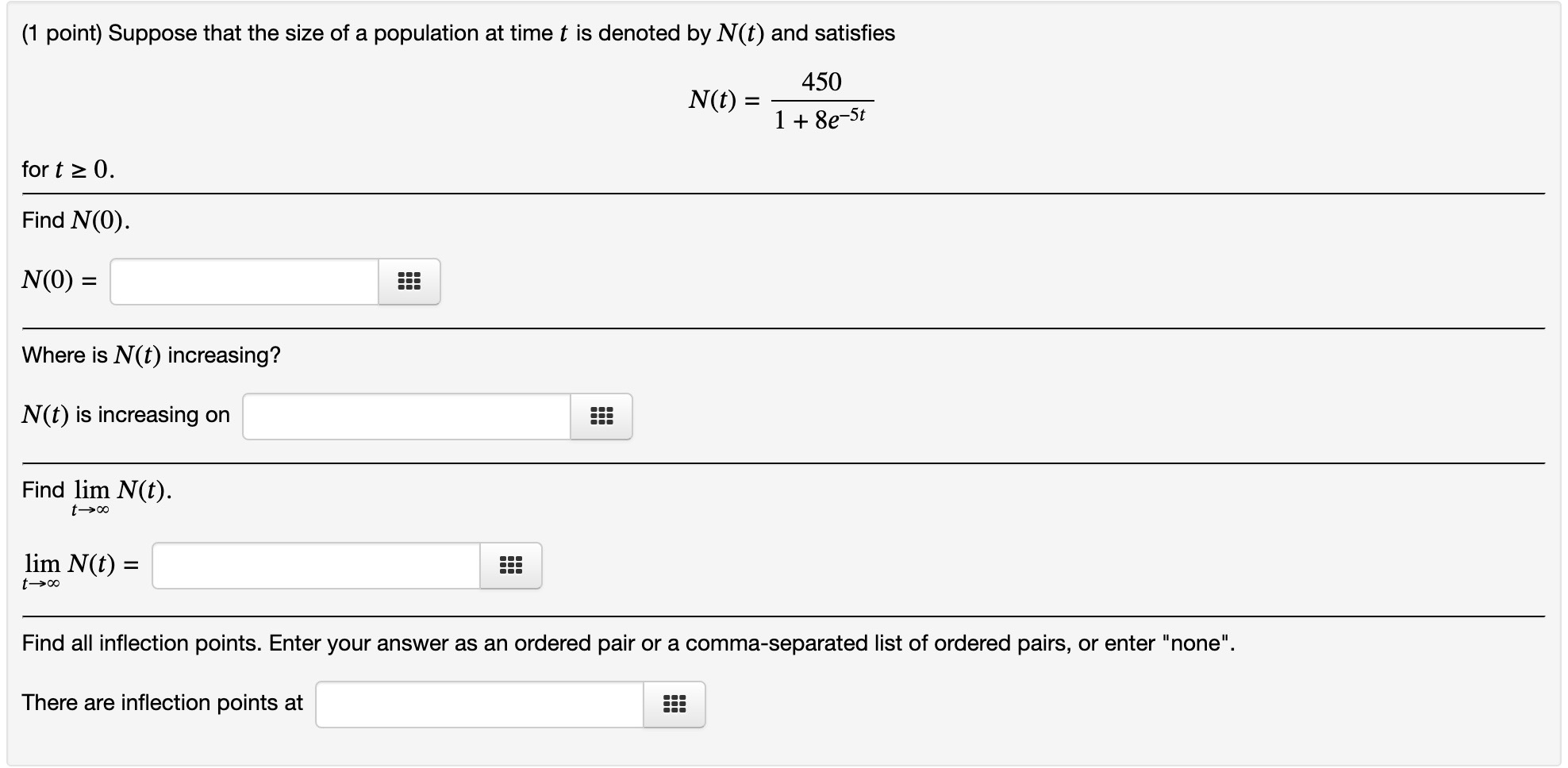
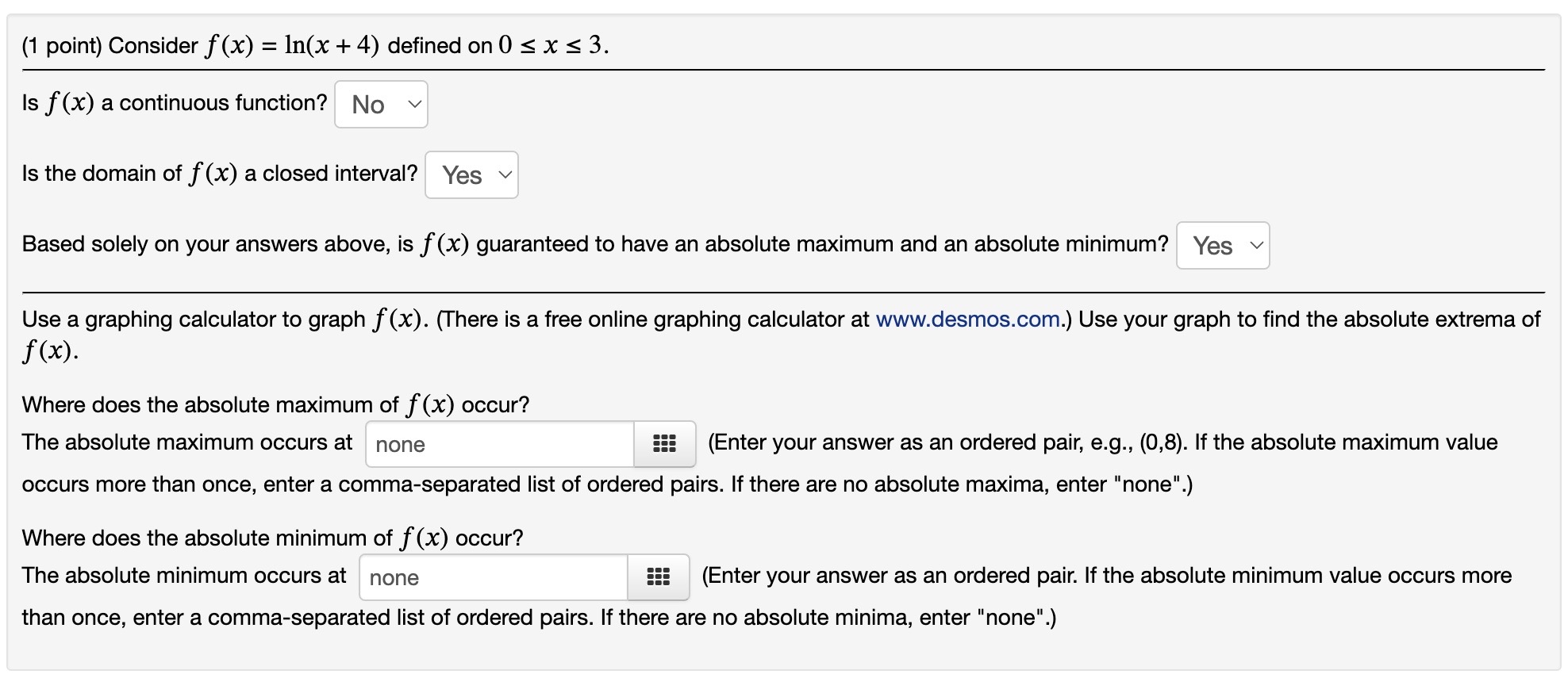
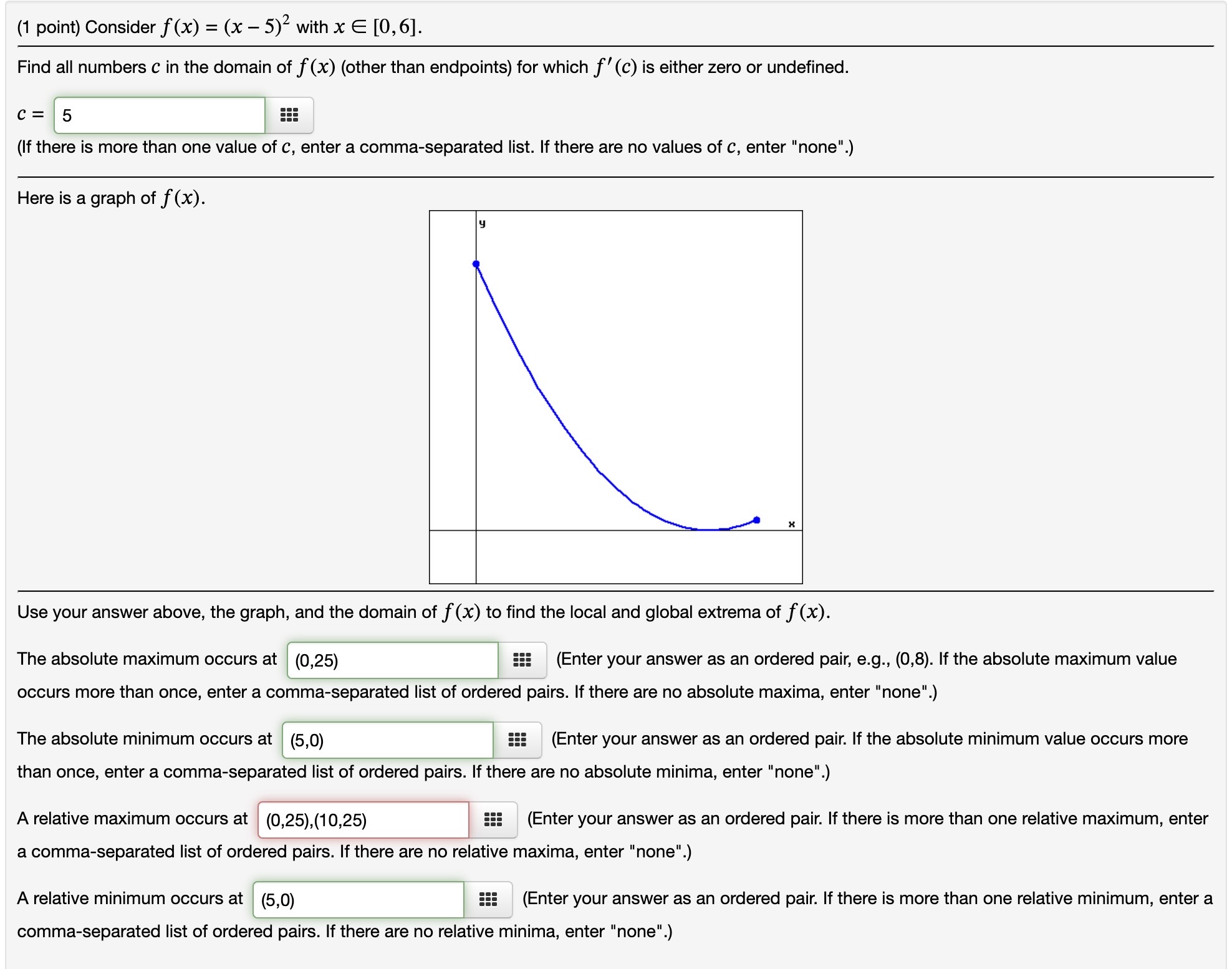
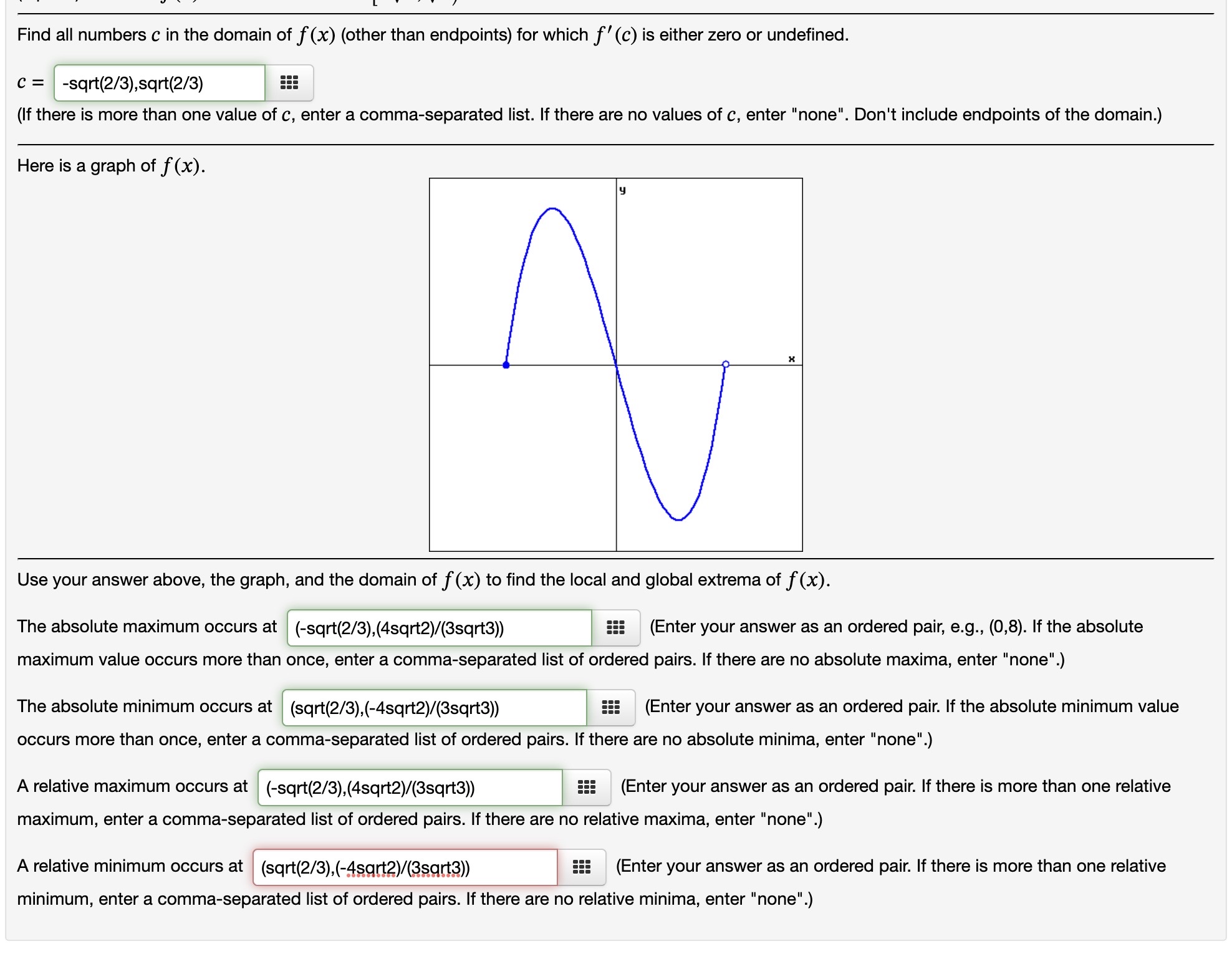
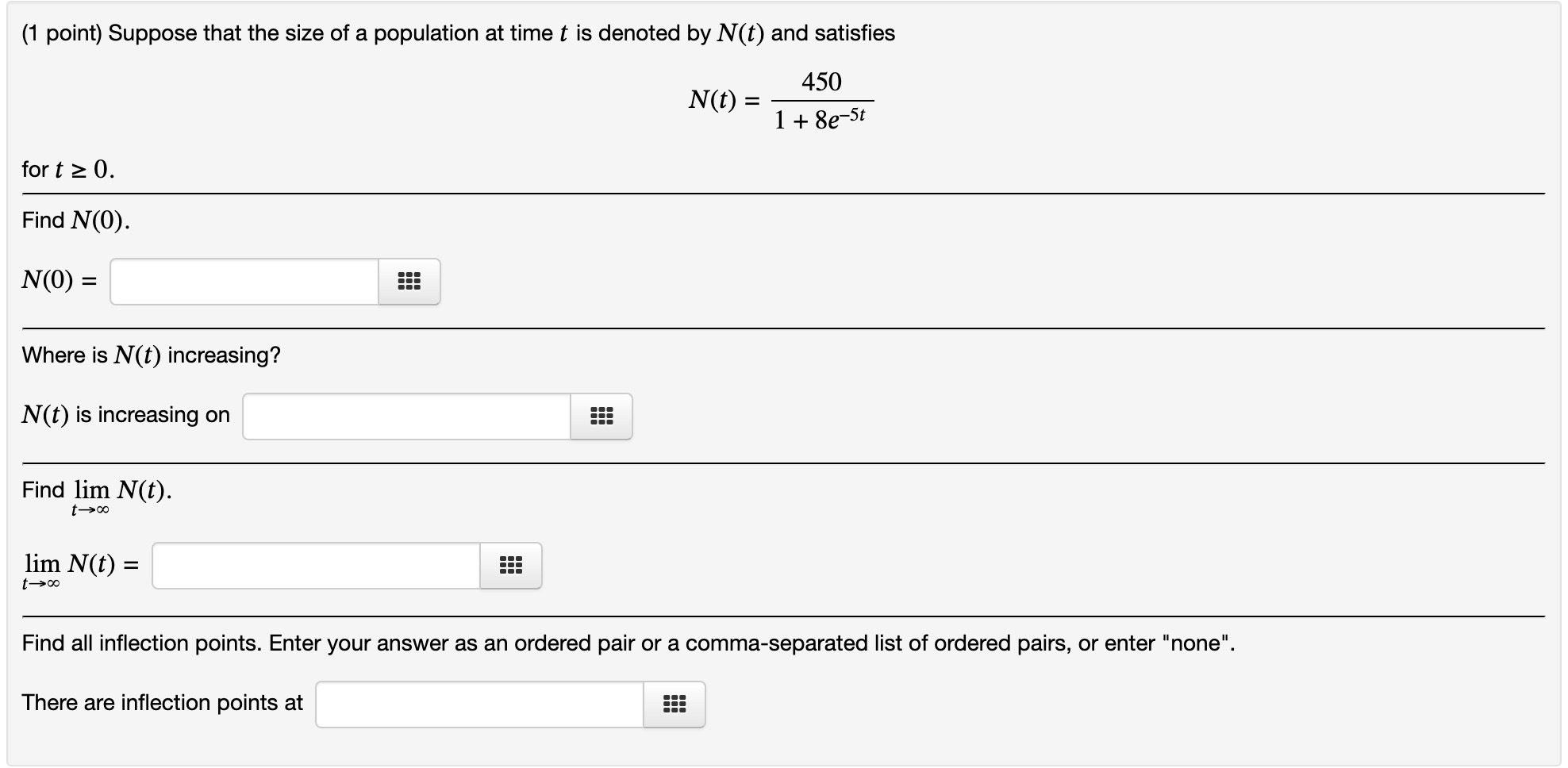
(1 point) Consider f(x) = 1n(x + 4) defined on 0 s x s 3. Is f(x) a continuous function? No v Is the domain of f(x) a closed interval? Yes v Based solely on your answers above, is f (x) guaranteed to have an absolute maximum and an absolute minimum? Yes v Use a graphing calculator to graph f(x). (There is a free online graphing calculator at www.desmos.com.) Use your graph to find the absolute extrema of f ()6)- Where does the absolute maximum of f(x) occur? The absolute maximum occurs at none 555 (Enter your answer as an ordered pair, e.g., (0,8). If the absolute maximum value occurs more than once, enter a commaseparated list of ordered pairs. If there are no absolute maxima, enter "none". Where does the absolute minimum of f(x) occur? The absolute minimum occurs at none EEE (Enter your answer as an ordered pair. If the absolute minimum value occurs more than once, enter a comma-separated list of ordered pairs. If there are no absolute minima, enter "none".) (1 point) Consider f(x) = (x 5)2 with x E [0,6]. Find all numbers C in the domain of f(x) (other than endpoints) for which f'(c) is either zero or undefined. C25 (If there is more than one value of c, enter a comma-separated list. If there are no values of 0, enter "none". Here is a graph of f(x). Use your answer above, the graph, and the domain of f(x) to find the local and global extrema of f(x). The absolute maximum occurs at (0,25) 555 (Enter your answer as an ordered pair, e.g., (0,8). If the absolute maximum value occurs more than once, enter a commaseparated list of ordered pairs. If there are no absolute maxima, enter "none". The absolute minimum occurs at (5,0) 555 (Enter your answer as an ordered pair. If the absolute minimum value occurs more than once, enter a commaseparated list of ordered pairs. If there are no absolute minima, enter "none".) A relative maximum occurs at } (0,25),(10,25) _ EEE (Enter your answer as an ordered pair. If there is more than one relative maximum, enter a comma-separated list of ordered pairs. If there are no relative maxima, enter "none".) A relative minimum occurs at (5,0) 5!! (Enter your answer as an ordered pair. ll there is more than one reiative minimum, enter a comma-separated list of ordered pairs. If there are no relative minima, enter "none". 0', L"'I Find all numbers C in the domain of f(x) (other than endpoints) for which f'(c) is either zero or undefined. C = sqrt(2/3),sqrt(2/3) iii (If there is more than one value of c, enter a comma-separated list. If there are no values of c, enter "none". Don't include endpoints of the domain.) Here is a graph of f(x). Use your answer above, the graph, and the domain of f(x) to find the local and global extrema of f(x). The absolute maximum occurs at (-sqrt(2/3),(4sqr12)/(33qrt3)) 555 (Enter your answer as an ordered pair, e.g., (0,8). If the absolute maximum value occurs more than once, enter a commaseparated list of ordered pairs. If there are no absolute maxima, enter "none". The absolute minimum occurs at (sqrt(2/3),(4sqr12)/(3sqrt3)) 555 (Enter your answer as an ordered pair. If the absolute minimum value occurs more than once, enter a commaseparated list of ordered pairs. If there are no absolute minima, enter "none". A relative maximum occurs at (sqrt(2/3),(4sqrt2)/(3sqrt3)) iii (Enter your answer as an ordered pair. If there is more than one relative maximum, enter a commaseparated list of ordered pairs. If there are no relative maxima, enter "none".) : l l A relative minimum occurs at l (sqr1(2/3),(4sqn2)/(3sqr13 iii (Enter your answer as an ordered pair. If there is more than one relative minimum, enter a comma-separated list of ordered pairs. If there are no relative minima, enter "none". (1 point) Suppose f (x) = x6 ln(x) . Find the intervals on which f is increasing or decreasing. f is increasing on ::: f is decreasing on EEE (Enter your answer using interval notation.) Find the local maximum and minimum values of f. Local maximum values are 5!! Local minimum values are iii (If there are none, enter "none". If there is more than one, enter a comma-separated list.) Find the intervais of concavity. f is concave up on f is concave down on ::: (Enter your answer using interval notation.) Find the inflection points of f. lnflection points are (Enter each inflection point as an ordered pair, like (3,5). If there is more than one, enter a commaseparated list of ordered pairs. If there are none, enter "none". Use your answers above to sketch the graph of y = f (x). (1 point) Suppose f(x) = {ex. Find the intervals on which f is increasing or decreasing. f is increasing on ::: f is decreasing on 5!! (Enter your answer using inten/al notation.) Find the local maximum and minimum values of f. Local maximum values are 5!! Local minimum values are ::: (If there are none, enter "none". If there is more than one, enter a comma-separated list.) Find the intervals of concavity. f is concave up on f is concave down on ::: (Enter your answer using interval notation.) Use your answers above to sketch the graph ofy = f(x). (1 point) Suppose that the size of a population at time t is denoted by N(t) and satisfies 450 N(t) = 1 + 8e-5t for t 2 0. Find N(0). N(0) = Where is N(t) increasing? N(t) is increasing on Find lim N(t). lim N(t) = 1 - 0o Find all inflection points. Enter your answer as an ordered pair or a comma-separated list of ordered pairs, or enter "none". There are inflection points at