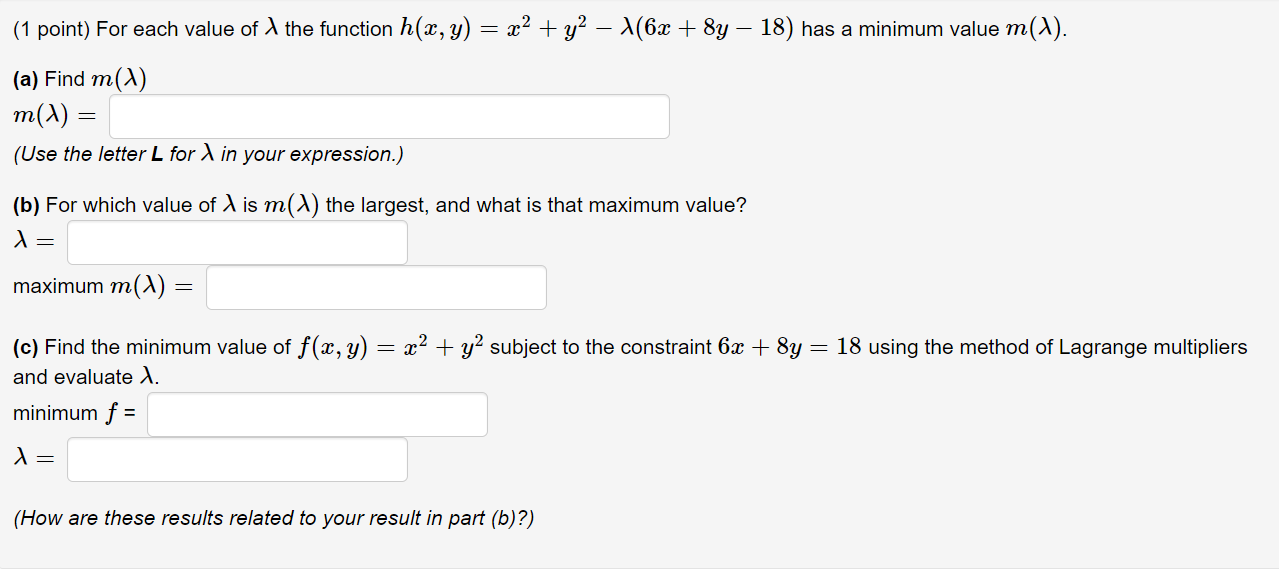
(1 point) For each value of A the function h(:c, y) = 3:2 + :92 M63 + 8y 18) has a minimum value m()\\). (a) Find m(/\\) m()\\) : { Use the letter L for z\\ in your expression.) (b) For which value of A is m()\\) the largest, and what is that maximum value? A: maximum m()\\) : (c) Find the minimum value of ax, y) : m2 + y2 subject to the constraint 6:1: + By : 18 using the method of Lagrange multipliers and evaluate A. minimum 1' = A: {How are these results related to your result in part (12)?)