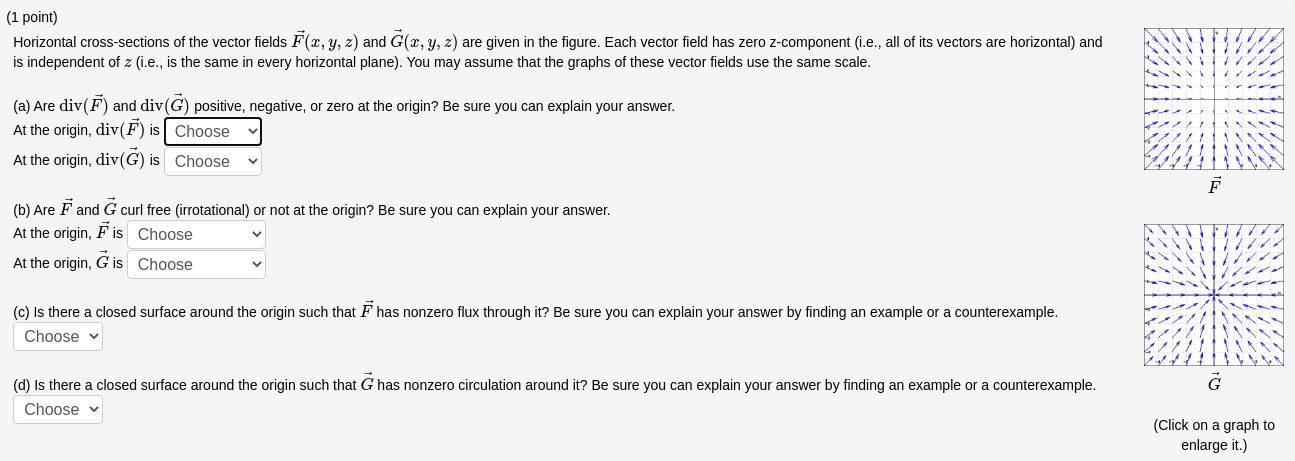
(1 point) Horizontal cross-sections of the vector fields F(x, y, z) and G(x, y, z) are given in the figure. Each vector field has zero z-component (i.e., all of its vectors are horizontal) and is independent of z (i.e., is the same in every horizontal plane). You may assume that the graphs of these vector fields use the same scale. (a) Are div(F) and div(G) positive, negative, or zero at the origin? Be sure you can explain your answer. At the origin, div(F) is Choose At the origin, div(G) is Choose (b) Are F and G curl free (irrotational) or not at the origin? Be sure you can explain your answer. At the origin, F is Choose At the origin, G is Choose (c) Is there a closed surface around the origin such that F has nonzero flux through it? Be sure you can explain your answer by finding an example or a counterexample. Choose v (d) is there a closed surface around the origin such that G has nonzero circulation around it? Be sure you can explain your answer by finding an example or a counterexample. G Choose v (Click on a graph to enlarge it.)