$(1$ point$)$ In this problem we will crack RSA. Suppose the parameters for an instance of the RSA cryptosystem are $N=4661,e=5.(1$ point$)$ The speed of RSA hinges on the ability to do large modular exponentiations quickly.$(1$ point$)$ The Chinese Remainder Theorem is often used as a way to speed up modular exponentiation. In this problem we go through the procedure of using CRT$.$

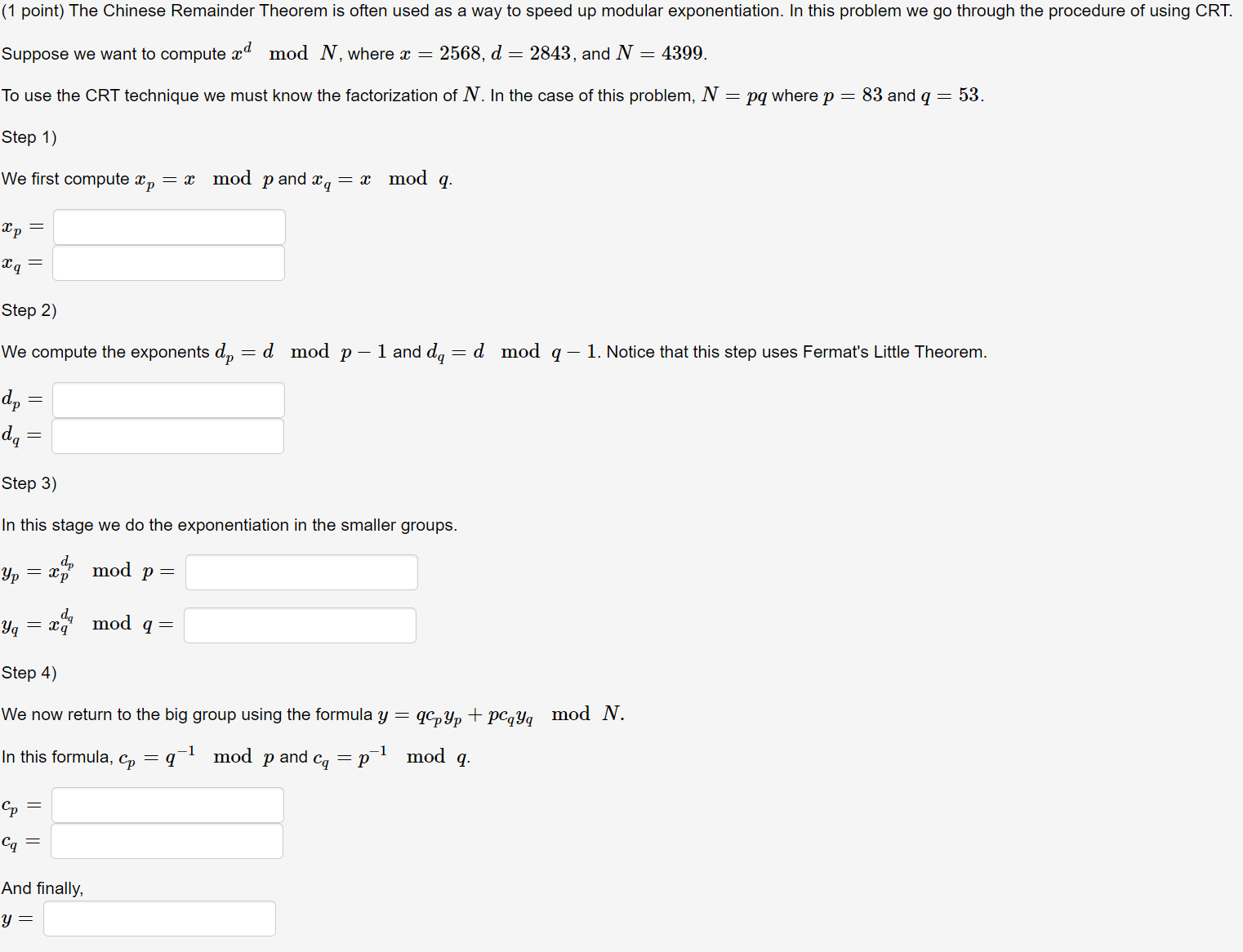
Suppose we want to compute $x^d$modN, where $x=2568,d=2843,$ and $N=4399.$

To use the CRT technique we must know the factorization of $N.$ In the case of this problem, $N=pq$ where $p=83$ and $q=53.$

Step $1)$

We first compute $x_p=x,$modp and $x_q=$xmodq.

$x_p=$

$x_q=$

Step $2)$

We compute the exponents $d_p=$dmodp$-1$ and $d_q=$dmodq$-1.$ Notice that this step uses Fermat's Little Theorem.

$d_p=$

$d_q=$

Step $3)$

In this stage we do the exponentiation in the smaller groups.

$y_p=x_p^{d_p}$modp$=$

$y_q=x_q^{d_q}$modq$=$

Step $4)$

We now return to the big group using the formula $y=q{c}_p{y}_p+p{c}_q{y}_q$modN.

In this formula, $c_p=q^{-1}$modp and $c_q=p^{-1}$modq.

$c_p=$

$c_q=$

And finally,

$y=$

While $e$ can be made small, $d$ generally cannot.

A popular method for fast modular exponentiation is the Square and Multiply algorithm.

Suppose that $N=19511$ and $d=3845.$ We want to use the Square and Multiply algorithm to quickly decrypt $y=17512.$

a$)$ Express $d$ as a binary string $($e$.$g$\mathrm{.}10110110).SQ\frac{,}{M}UL,SQ,SQ,SQ\frac{,}{M}UL,SQ,SQ\frac{,}{M}UL,SQ,SQ.$

c$)$ What is $x=y^d$modN $?$

We have obtained some ciphertext $y=1046.$

a$)$ Factor $N=4661$ into its constituent primes $p$ and $q.$

min$(p,q)=$

max$(p,q)=$

b$)$ Compute $(N).$

$(4661)=$

c$)$ Compute $d,$ the decryption exponent.

$d=$

d$)$ Decrypt $y=1046$ to find the plaintext.

$x=$