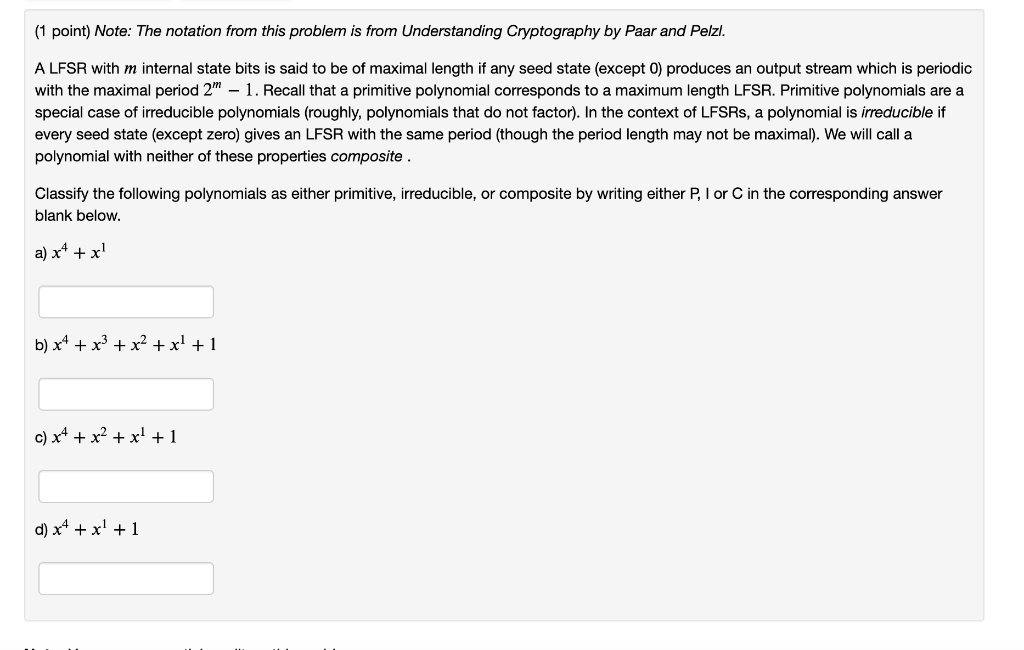
(1 point) Note: The notation from this problem is from Understanding Cryptography by Paar and Pelzl. We conduct a known-plaintext attack against an LFSR. Through trial and error we have determined that the number of states is m = = 4. The plaintext given by 10111001 = xox1x2x3X4X5X6X7 when encrypted by the LFSR produced the ciphertext 01011010 = yo Y1 y2 Y3 Y3 Y5 Y6 Y7. What are the tap bits of the LFSR? Please enter your answer as unspaced binary digits (e.g. 0101 to represent P3 = 0, P2 = 1, P1 = 0, po = 1). (1 point) Note: The notation from this problem is from Understanding Cryptography by Paar and Pelzl. A LFSR with m internal state bits is said to be of maximal length if any seed state (except 0) produces an output stream which is periodic with the maximal period 2 1. Recall that a primitive polynomial corresponds to a maximum length LFSR. Primitive polynomials are a special case of irreducible polynomials (roughly, polynomials that do not factor). In the context of LFSRs, a polynomial is irreducible if every seed state (except zero) gives an LFSR with the same period (though the period length may not be maximal). We will call a polynomial with neither of these properties composite. Classify the following polynomials as either primitive, irreducible, or composite by writing either P, I or C in the corresponding answer blank below. a) x4 + x1 b) x4 x2 + x1 + 1 c) x4 + x2 + x1 + 1 d) x4 + x + 1