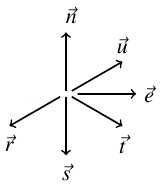
(1 point] Several unit vectors F, E, E, iii, and E in the xivplane [not threedimensional space} are shown in the gure. Using the geometric denition of the not product, are the following dot products positive, negative, or zero? You may.r assume that angles that looI-t the same are the same. {3 v 1.F--ii v v 2.5 F v v aft E v v do v v 5.F v v 5.5 E v v 13' E (1 point) Find the orthogonal projection (and the associated scalar component) of b onto a, where a = (-1, 1, 2) and b = (-1, 5, 9) 1. comp, b = 2. proj, b =(1 point) Find two unit vectors orthogonal to a = (-2, 5, -5) and b = (4, 0, -2) Enter your answer so that the first vector has a positive first coordinate First Vector: ( Second Vector: ((1 point) Let A = (2, -1, 2), B = (1, -3, 6), C = (3, -8, 1), and D = (4, -6, -3). Find the area of the parallelogram determined by these four points, the area of the triangle ABC, and the area of the triangle ABD. Area of parallelogram ABCD = Area of triangle ABC = Area of triangle ABD =(1 point) Suppose v = (3, -1, 3). Then (-6, 2, -6) is ? v to v (-4, -1, 1) is ? to v (5, -1, 4) is ? to v (4, -27, -13) is ? to v\f