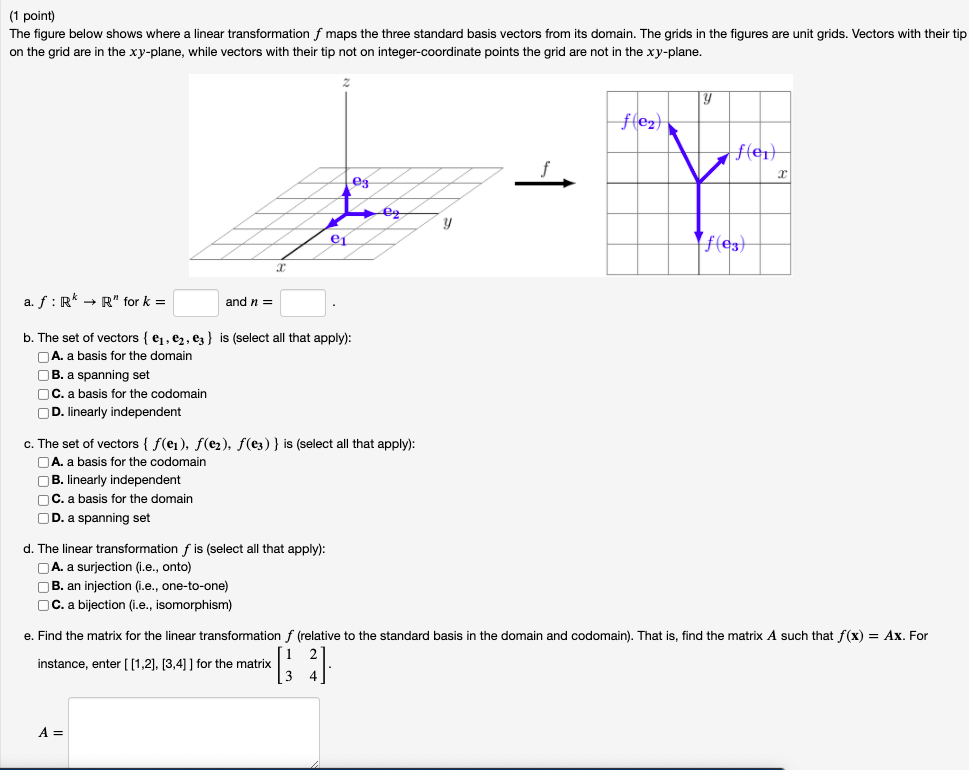
(1 point) The figure below shows where a linear transformation / maps the three standard basis vectors from its domain. The grids in the figures are unit grids. Vectors with their tip on the grid are in the xy-plane, while vectors with their tip not on integer-coordinate points the grid are not in the xy-plane. fez) flen) ez e1 a. f : R* - R" for k = and n = b. The set of vectors { e] , ez, e} } is (select all that apply): A. a basis for the domain OB. a spanning set OC. a basis for the codomain OD. linearly independent c. The set of vectors { f(e1 ), f(e2 ), f(es) } is (select all that apply): OA. a basis for the codomain OB. linearly independent OC. a basis for the domain OD. a spanning set d. The linear transformation f is (select all that apply): QA. a surjective., onto) OB. an injection (i.e., one-to-one) OC. a bijection (i.e., isomorphism) e. Find the matrix for the linear transformation (relative to the standard basis in the domain and codomain). That is, find the matrix A such that f (x) = Ax. For instance, enter [ [1,2], [3,4] ] for the matrix A =