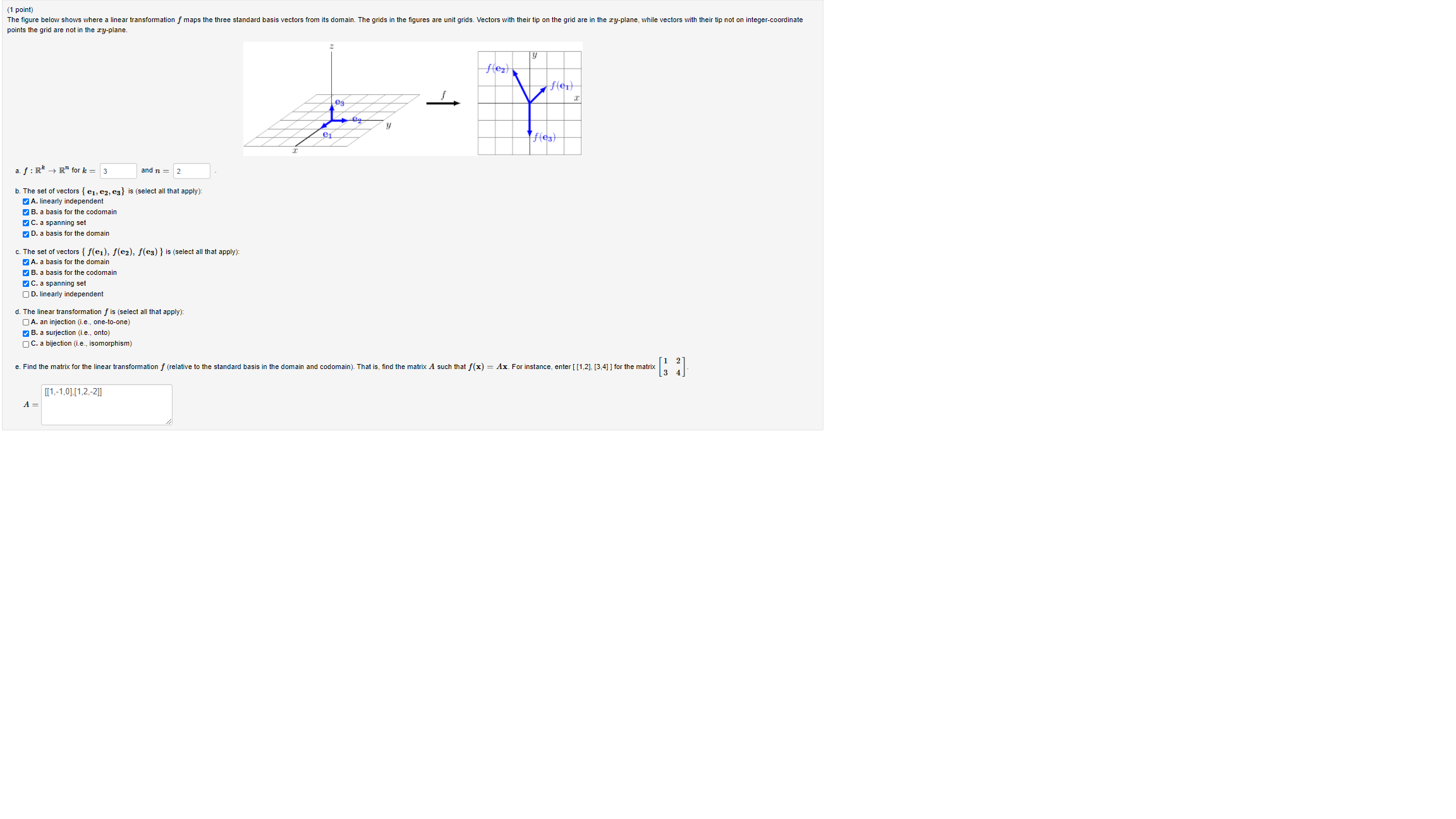
Question: asdfasdfas (1 point) The figure below shows where a linear transformation f maps the three standard basis vectors from its domain. The grids in the
asdfasdfas
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


