1. Process Optimization (linear programming) is technique used to determine a way to achieve the optimal outcome. In this part of the assignment, our fictitious health system, VVH, tries to figure out the right case mix for DRGs in order to maximize its profits. The controllable inputs (decision variables) are the numbers of cases for different DRGs. Two types of constraints limit the numbers of cases. One is that VVH has to provide minimum numbers of cases for these DRGs. The other type of constraint requires that the resources used to provide these services cannot exceed available resources. See the detailed information on pages 153-155 of the textbook. With the current resources, VVH can achieve a maximum profit of $43,454. Now VVH has decided to convert 15 routine bed days to ICU bed days for a cost of $2,000. The data for the first part of the assignment is stored in the worksheet Optimization of the file Group Assignment 2_Excel.xlsl and use Excel solver to find answers to the following questions:

a) What is the maximum profit after VVH makes the change?

b) What are the optimal cases for respiratory, coronary surgery, birth/delivery, and alcohol/drug abuse DRGs?

c) If a variable and its constraint have been met exactly, they are binding. Otherwise, they are not binding and the positive difference is called slack. What clinical resources have slack?

d) Reduced gradient is an estimate of how much the objective function will change when forcing in one unit of a decision variable that is binding. What is the reduced gradient for an additional respiratory DRG case?

e) Lagrange Multiplier is also called shadow price, which indicate the change in the objective function when adding one unit of the resource. What is the shadow price for an additional unit of Diagnostic Services (hours)? You need to load the Solver add-in if you havent done so. Click the File tab, and then click Options. Click Add-Ins, and then in the Manage box, select Excel Add-ins. Click Go. In the Add-Ins available box, select the Solver Add-in check box, and then click OK. After you load the Solver, click the cell I9 and then choose Data -> Solver. A dialogue box Solver Parameters should pop up.

The setup should be there already. But if not, you need to enter the following information:

Set target cell: $I$9

Equal to: Max

By changing cells: $B$13:$E$13

Subject to the constraints:

$B$13>=$B$11

$C$13>=$C$11

$D$13>=$D$11

$E$13>=$E$11

$I$4

$I$5

$I$6

$I$7

Click on Solve in the Solver Parameters dialogue box. After a short while, the Solver Results dialogue box should pop up. In the Reports group, select Answer and Sensitivity. Click OK. The value of the cell I9 should be greater than $43,454.

Now modify the numbers of ICU bed days and routine bed days. Solve the model again. You should be able to find the answers to the above questions in the Answer and Sensitivity reports.

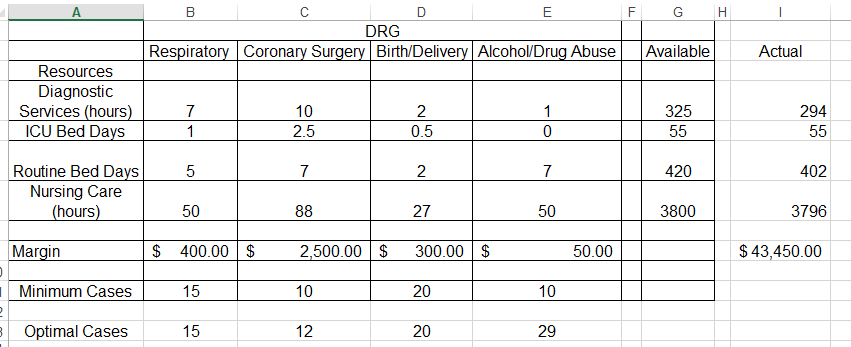
G H DRG Respiratory Coronary Surgery Birth/Delivery Alcohol/Drug Abuse Available Actual Resources Diagnostic Services (hours) ICU Bed Days 325 294 2 0.5 55 55 420 402 Routine Bed Days Nursing Care (hours) 50 3800 3796 Margin $ 400.00 $ 2,500.00 $ 300.00 $ 50.00 $ 43,450.00 Minimum Cases 15 20 10 12 3 Optimal Cases 15 20 20 29 G H DRG Respiratory Coronary Surgery Birth/Delivery Alcohol/Drug Abuse Available Actual Resources Diagnostic Services (hours) ICU Bed Days 325 294 2 0.5 55 55 420 402 Routine Bed Days Nursing Care (hours) 50 3800 3796 Margin $ 400.00 $ 2,500.00 $ 300.00 $ 50.00 $ 43,450.00 Minimum Cases 15 20 10 12 3 Optimal Cases 15 20 20 29