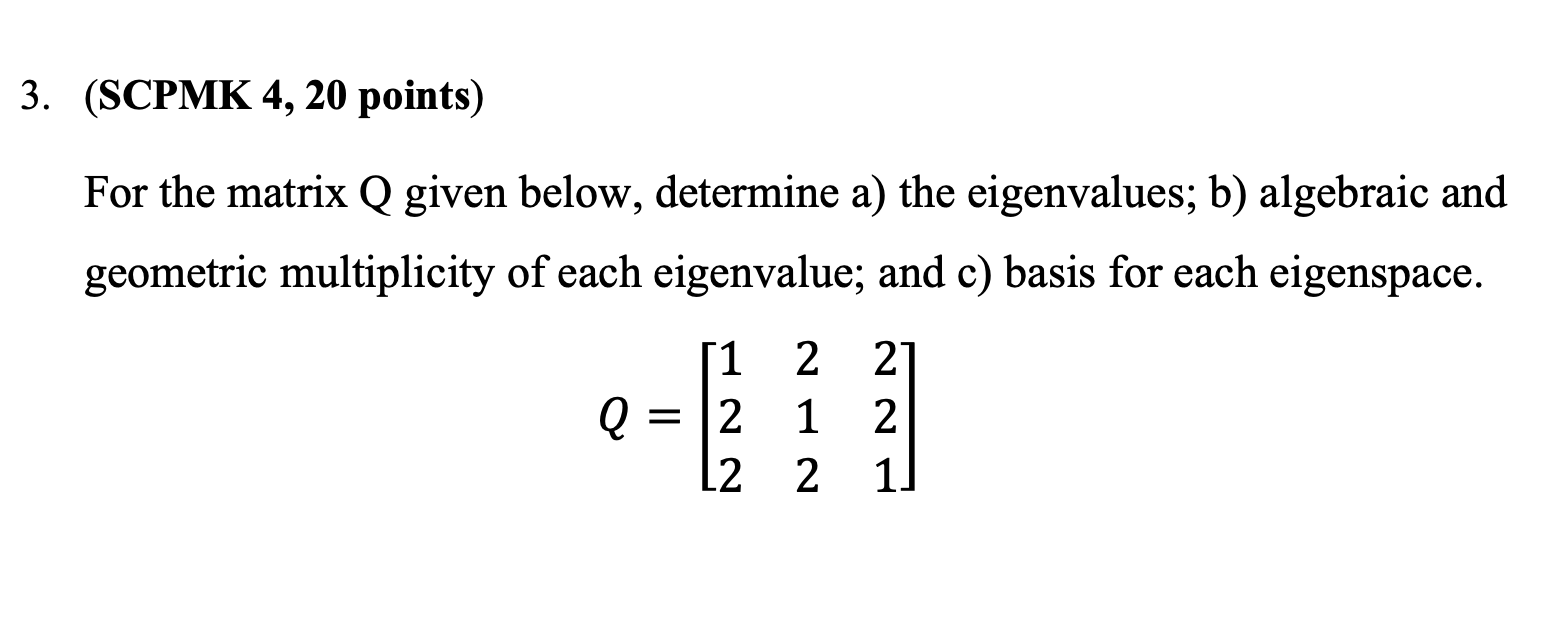
1. (SCPMK 3, 17 points) Let S = {(-1, 2, 3, 0), (2, 1, 5, -1), (3, 0, 2, 8), (6, 4, 15, 6)}. a. Determine a subset of S that forms a basis for the space spanned by S. b. If there is a vector in S that does not belong to the basis chosen in part a, determine its coordinate vector relative to the basis. 2. (SCPMK 4, 30 points) The formula = ujV1 + 2uzV2 + U3V3 defines an inner product on R3, where u = (u1, U2, U3 ) and v = (V1, V2, V3 ). Consider the basis S = {w1, W2, W3), where w1 = (1,1,1), w2 = (1,1,0), and W3 = (1,0,0). a) Determine if S is an orthonormal basis relative to the stated inner product. b) If S is not orthonormal, build an orthonormal basis S' using the Gram- Schmidt process and normalization.3. (SCPMK 4, 20 points) For the matrix Q given below, determine a) the eigenvalues; b) algebraic and geometric multiplicity of each eigenvalue; and 0) basis for each eigenspace. 122 Q=212 221 4. (SCPMK 5, 20 points) Let T: R3 > R2 be a linear transformation and let are .( >=e> -. T(L'1'.D=- a. Knowing that {(1, 1, 1), (1, 1, 0), (0, 1, 1)} forms a basis for R3, determine the explicit formula for T, that is, T (X1, X2, X3), for any vector (X1, X2, X3) in R3. 1 1 0 2 b. Use the formula derived in part a to nd T Q 3 D. 1 c. Determine bases for ker(T) and R(T) and specify their dimensions. 5. (SCPMK 5, 13 points) 2ab a. Let T: R2 > R2 be a linear operator such that T ([2]) = 3a + b 1. Find the det (T) using the basis B = {(2, 0), (0, 2)}. b. Explain why the determinant of a linear operator does not depend on the choice of basis, that is, it results in the same number using any valid basis