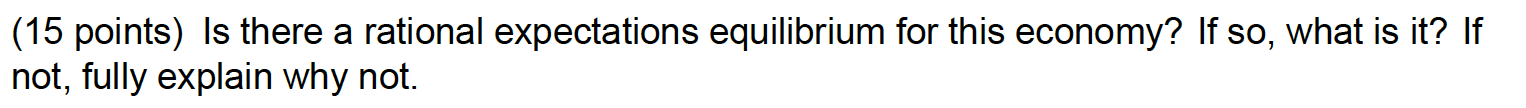
1. Suppose there are two traders, two commodities x = (1, x2) and two potential states at time 1 s E {1, 2}. At time -1, both traders believe each state is equally likely at time 1; at time 0, however, trader 1 receives a private signal that fully informs him about the state at time 1. That is, at time 0, agent 1 either receives a the signal of = (1, 0) that state 1 is occurring with probability 1 or he receives the signal of = (0, 1) that state 2 is occurring with 100 percent probability. The second trader, however, receives the signal o2, that has no special information. Assume state-independent endowments are w1 = W2 = (3, 3) and define utilities as v1(x) = (3 - s) log x 1 + s log(2 2) and V2 (X) = s log(1) + (3 - s) log(22).(15 points) Is there a rational expectations equilibrium for this economy? If so, what is it? If not, fully explain why not