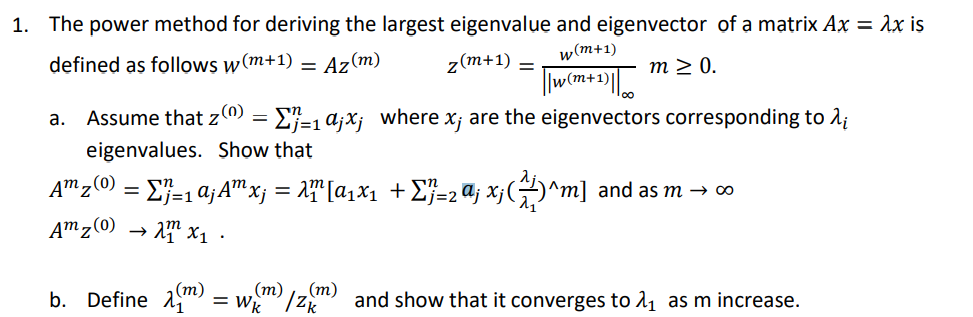
1 . The power method for deriving the largest eigenvalue and eigenvector of a matrix AX = 1x is defined as follows w ( m + 1 ) = AZ ( m ) z ( m + 1 ) - w ( m + 1 ) | w ( m + 1 ) |` m > O . a. Assume that z(m) = Jim_` {} = 1 dix ; where * ; are the eigenvectors corresponding to di eigenvalues . Show that Am z 10) = LE= 1 a; Amx " x ; = 2^ [ a1 x 1 + 2j = 2 a j Xj( ` Ajj Am ] and as m + 00 Am z ( 0 ) - 172 x 1 . 6. Define A` ( m ) = WK ( m ) / Z K` ( m ) and show that it converges to A , as m increase