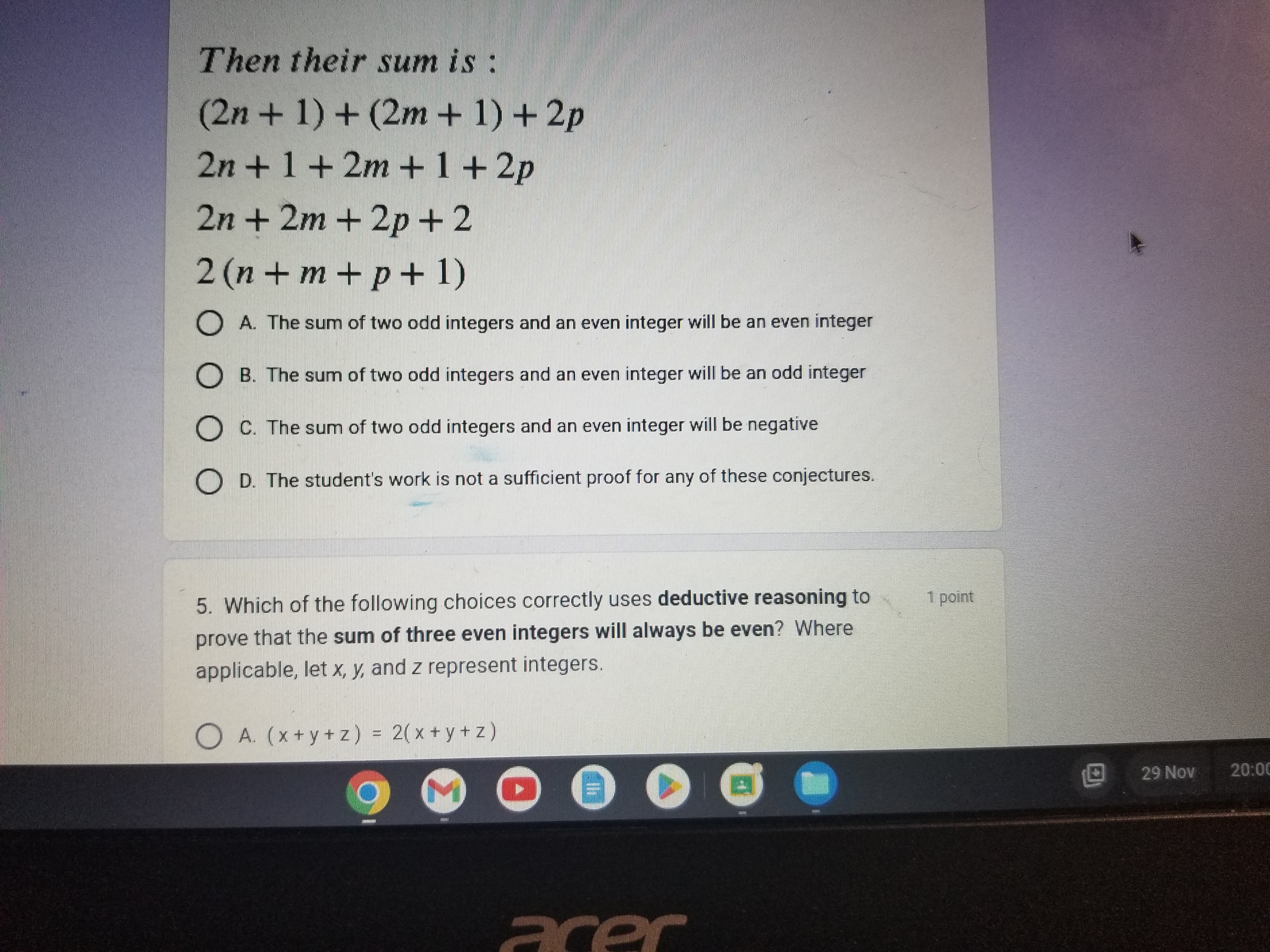
1. True or False: 1 point If deductive reasoning is done correctly, it can be used to prove that a conjecture is always valid. True False 2. Use the factual statements below to answer the question that follows: 1 point - All cats are mammals. All mammals are warm-blooded Garfield is a cat. A student made the following two deductions about Garfield: i) Garfield is a mammal ii) Garfield is warm-blooded Based on the information, which, if any, of the student's deductions are correct? 29 Nov 20:00 A 62. Use the factual statements below to answer the question that follows: 1 point - All cats are mammals. - All mammals are warm-blooded - Garfield is a cat. A student made the following two deductions about Garfield: 1) Garfield is a mammal 10) Garfield is warm-blooded Based on the information, which, if any, of the student's deductions are correct? A. Only i) is correct. B. Only ii) is correct. C. Both i) and ii) are correct. ( D. Neither i) nor ii) are correct. 3. A student was given the following factual statements 1 point 29 Nov 20:003. A student was given the following factual statements 1 point Math 20-2 students must have graphing calculators David owns a graphing calculator. The student then used deductive reasoning to draw the following conclusion: "Therefore, David is a Math 20-2 Student" If the student's reasoning is incorrect, explain why. If the student's reasoning is correct, answer by typing "Correct". Your answer 4. A student used deductive reasoning to prove a conjecture. Their correct 1 point proof is shown below. Which of the following conclusions can the student's proof be used to confirm? Let : 29 Nov2n + 1 be an odd integer 2m + 1 be another odd integer 23; be an even integer TEE}: their sumis: {23+1)+(2m+1)+2p 2E+1+2m+1+2p 2n+2m+2p+2 2(n+m+p+1) Q A The sum of two odd integegs and an even integer will be an even integer W a W Then their sum is : (2n + 1) + (2m + 1) + 2p 2n + 1+ 2m + 1+ 2p 2n + 2m + 2p + 2 2 (n + m+ p+1) A. The sum of two odd integers and an even integer will be an even integer O B. The sum of two odd integers and an even integer will be an odd integer O C. The sum of two odd integers and an even integer will be negative D. The student's work is not a sufficient proof for any of these conjectures. 5. Which of the following choices correctly uses deductive reasoning to 1 point prove that the sum of three even integers will always be even? Where applicable, let x, y, and z represent integers. O A. ( x + y + z ) = 2( x + y+z ) 29 Nov 20:0 acer5. Which of the following choices correctly uses deductive reasoning to 1 point prove that the sum of three even integers will always be even? Where applicable, let x, y, and z represent integers. O A. ( x + y+z) = 2(x+y+z) O B. 2+4+6 = 12 and 4+6 +8 = 18 O C. 2x + 2y + 2z = 2(x + y+ z) D. None of the above 6. A teacher asked her students to prove that the result will always be 7 if you 1 point follow these steps: 1. Choose any number 2. Add 2 3. Multiply by 2 29 Nov 20:00 A 9 M acer6. A teacher asked her students to prove that the result will always be 7 if you 1 point follow these steps: 1. Choose any number 2. Add 2 3. Multiply by 2 4. Add 3 5. Subtract 2 times the original number Sally's attempt to prove that this works is shown below. If Sally made a mistake, in which step did the mistake occur? 1. Let n be the original number. 2. Add 2: n + 2 3. Multiply by 2: 2(n + 2) = 2n + 4 4. Add 3: 2n + 4 + 3 = 2n+ 7 5. Subtract two times the original number: 2n + 7 - 2n = 7 A. Sally made a mistake in Step 2 B. Sally made a mistake in Step 3 C. Sally made a mistake in Step 4 O D. Sally did not make an error, this is a correct proof. 29 Nov 20:01 A G GB V O acerEE 1. Let n be the original number. 2. Add 2: n + 2 3. Multiply by 2: 2(n + 2) = 2n + 4 4. Add 3: 2n + 4 + 3 =2n +7 5. Subtract two times the original number: 2n + 7 - 2n = 7 A. Sally made a mistake in Step 2 B. Sally made a mistake in Step 3 C. Sally made a mistake in Step 4 O D. Sally did not make an error, this is a correct proof. Upload photo(s) or scan(s) of your work for this assignment. 1 Add file Submit Clear form Never submit passwords through Google Forms This form was created inside of EPS. Report Abuse Google Forms 29 NOV