Question: 1) Use a flagpole model to prove that n + 1 3 = Xn1 k=1 k(n k). (please see the attachment for more details about

1) Use a flagpole model to prove that n + 1 3 = Xn1 k=1 k(n k).

(please see the attachment for more details about this question)

= Xn1 k=1 k(n k).(please see the attachment for more details about

$this question) \fA donut shop sells 4 kinds of donuts: chocolate, glazed,$

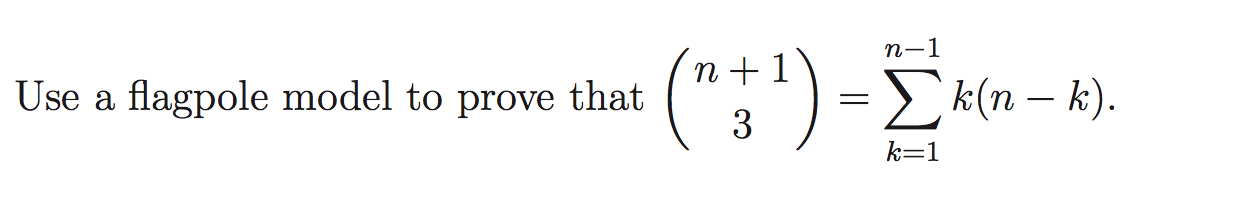
\fA donut shop sells 4 kinds of donuts: chocolate, glazed, jelly and sugar. How many different ways are there to buy 10 donuts a) with no restrictions? b) including at least 2 jelly and 3 glazed? 0) including no more than 5 chocolate? There are 7 people (3 men and 4 women) at a dinner party. In how many ways can they be seated around a circular table if a) there are no restrictions? b) no two men can be seated side by side? (3) Eric and Jean insist on sitting next to each other? 10. How many paths, always moving right or upward, join A to B in the following street patterns: a) B(10, 6) b) .B(9, 6) i i A(0, 0) A(0, 0) Hint: All paths must go through Hint: Compared to a complete grid, the point (6, 4) how many paths have been removed? 11. How many permutations of the multiset {314, 53,80} are there with: a) no restrictions? b) no adjacent As

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Please see attachment. All three question need to be answered in narrative format. If you have questions, just let me know. Normal requirement for references are 2 outside our course text....

Explain informally the difference between Godel's completeness theorem and his first incompleteness theorem. [8 marks] (b) State the meaning of Hoare triples {P} C {Q} in separation logic. [3 marks]...

Convert 2013 Tax Form 1040, Schedule A, Schedule B, Schedule C, Schedule D and Schedule SE forms into into 2020 1040, Schedule A, Schedule B, Schedule C, Schedule D and Schedule SE forms. Information...

Use the 2019 tax tables, available online Instructions Comprehensive Problem 1 - Part 3: Form 2441 (page 1), Schedule E, Form 4562, Child Tax Credit Worksheet, Form 8995, and schedule 8812. Note:...

I need help working through this problem. Most of the work I have completed but I need help ensuring that my answers are correct before submitting the assignment. I have attached the problem...

For the year 2018 i need Marias: -1040 -Schedule 1 -Schedule 4 -Schedule 5 -Schedule C -Schedule SE Please provide the correct numbers and properly written for the above forms. All the information is...

Richard McCarthy (born 2/14/1965; Social Security number 100-10-9090) and Christine McCarthy (born 6/1/1967; Social security number 101-21- 3434) have a 19-year-old son (born 10/2/2000 Social...

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

Question 1: Copy and Paste Go URL Link: https://www.irs.gov/pub/irs-pdf/f8949.pdf https://www.irs.gov/pub/irs-pdf/f1040.pdf https://www.irs.gov/pub/irs-pdf/f1040s1.pdf...

Write a C++ program to input two numbers, perform arithmetic operations on them and display the numbers and the results on the screen.

Faucette Chemical Company makes a variety of cosmetic products, one of which is a skin cream designed to reduce the signs of aging. Faucette produces a relatively small amount (15,000 units) of the...

( a ) Identify the key financial indicators ( e . g . , book value per share, earnings per share, liquidity ) from the case study that significantly influence market capitalization in Malaysian...

Which type of fraud is usually committed by industry insiders? Fraud for housing Fraud for profit Fraud for property Fraud for occupancy