1) Write a Python script that defines the system of equations and its Jacobian, sets the arguments for Newton-Raphson iteration and calls the function NR.py . Make sure your script prints out the residual and approximate error at every Newton-Raphson step, as well as the final result. Set both tolerances to 1012 .Please use the template down below.

2) Judging by the sequence of residuals, would you say that Newton-Raphson iteration has the same rate of convergence as Newton iteration?

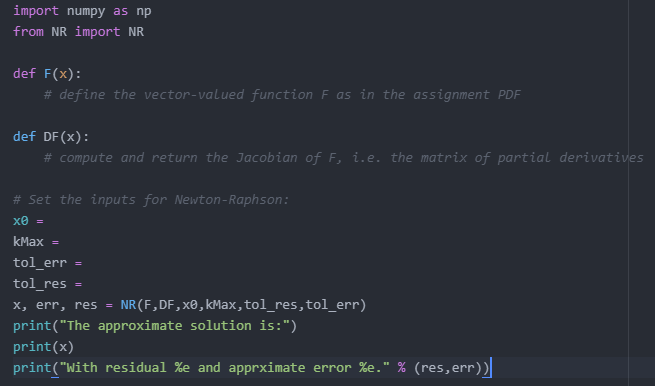
import numpy as np from NR import NR

def F(x): # define the vector-valued function F as in the assignment PDF

def DF(x): # compute and return the Jacobian of F, i.e. the matrix of partial derivatives

# Set the inputs for Newton-Raphson: x0 = kMax = tol_err = tol_res = x, err, res = NR(F,DF,x0,kMax,tol_res,tol_err) print("The approximate solution is:") print(x) print("With residual %e and apprximate error %e." % (res,err))

code for NR.py :

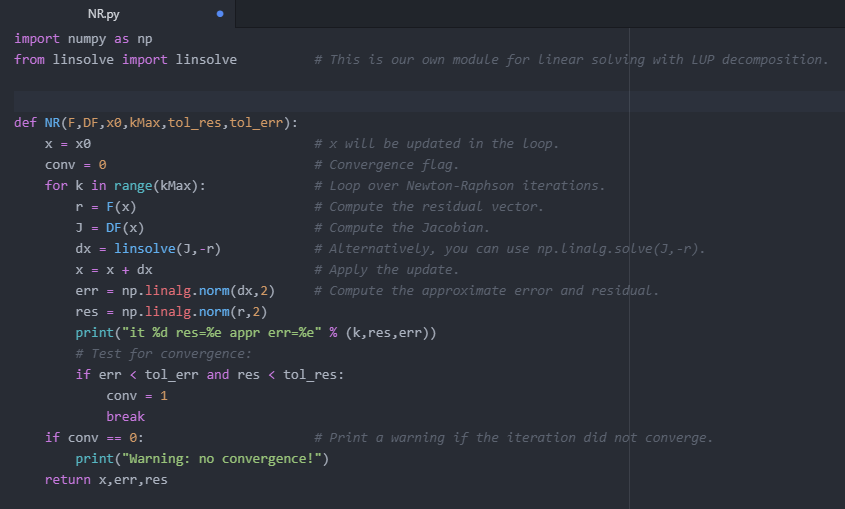
code for linsolve:

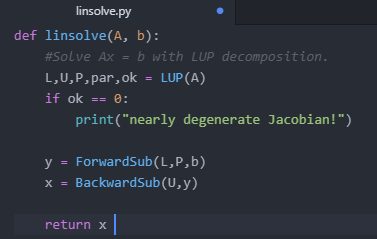
Consider the following system of equations: -2323 - 321+2=0 1129 - 41113 -12 +1 = 0 4.01.12 +213 - X3 = 0 There exists a solution close to r = (7,0,0) import numpy as np from NR import NR def F(x): # define the vector-valued function F as in the assignment PDF def DF(x): # compute and return the Jacobian of F, i.e. the matrix of partial derivatives # Set the inputs for Newton-Raphson: x = kMax = tol_err tol_res x, err, res - NR(E,DF,x0, kMax, tol_res, tol_err) print("The approximate solution is:") print(x) print("With residual %e and apprximate error %e." % (res, err)) NR.py import numpy as np from linsolve import linsolve # This is our own module for Linear solving with LUP decomposition. r = err = def NR(E,DF,x0, kMax, tol_res, tol_err): x = xD # x will be updated in the Loop. cony = 0 # Convergence flag. for k in range(kMax): # Loop over Newton-Raphson iterations. F(x) # Compute the residual vector. J DF(x) # Compute the Jacobian. dx linsolve(),-r) # Alternatively, you can use np.Linalg.solve(J,-r). X = X + dx # Apply the update. np.linalg.norm(dx, 2) # Compute the approximate error and residual. res = np.linalg.norm(r,2) print("it %d res=%e appr err=%e" % (k,res, err)) # Test for convergence: if err