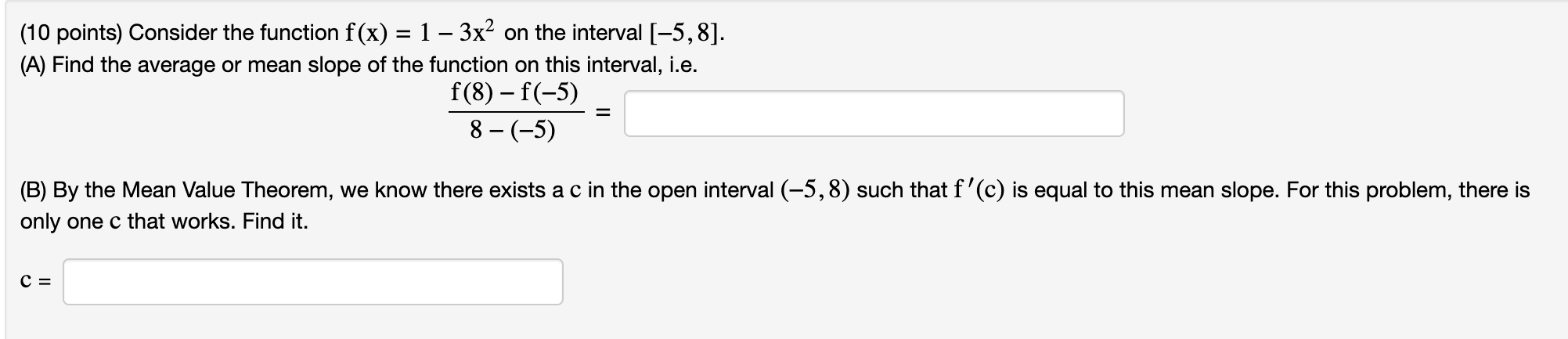
Question: (10 points) Consider the function f(x) = 1 3x2 on the interval [5, 8]. (A) Find the average or mean slope of the function on
![interval [5, 8]. (A) Find the average or mean slope of the](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6661c15ec3682_5266661c15ead221.jpg)




![+ 5 on the interval [4, 9]. Find the average or mean](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6661c160909ec_5286661c16077951.jpg)
(10 points) Consider the function f(x) = 1 3x2 on the interval [5, 8]. (A) Find the average or mean slope of the function on this interval, i.e. f(8)f(5) _ 8 (5) ' (B) By the Mean Value Theorem, we know there exists a c in the open interval (5, 8) such that f'(c) is equal to this mean slope. For this problem, there is only one c that works. Find it. c: (10 points) Consider the function foo = 2x3 9x2 24x + 5 on the interval [4, 9]. Find the average or mean slope of the function on this interval. Average slope = By the Mean Value Theorem, we know there exists at least one C in the open interval (4, 9) such that f'(c) is equal to this mean slope. Find all values of c that work and list them (separated by commas) in the box below. List of numbers: (1 0 points) Find all numbers (2 that satisfy the conclusion of the Mean Value Theorem for the following function and interval. Enter the values in increasing order and enter N in any blanks you don't need to use. f(x) = 63" , [0,6] (1 0 points) Find all numbers c that satisfy the conclusion of Rolle's Theorem for the following function and interval. Enter the values in increasing order and enter N in any blanks you don't need to use. f(x) = 7 sin(2nx),[1,1]
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


