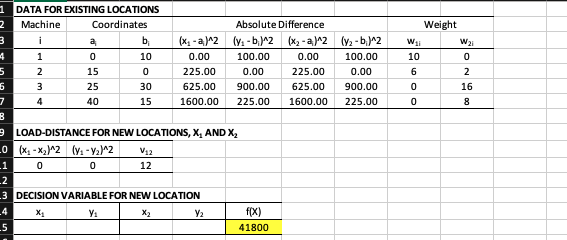
10.14b Use Solver for squared euclidean solution. Note that the current Excel spreadsheet is for two new machines/locations. For this problem you must change the Excel spreadsheet to adjust for a 3rd machine. Start with x = 0 and y = 0

DATA FOR EXISTING LOCATIONS \begin{tabular}{|c|c|c|c|c|c|c|c|c|c|} \hline Machine & \multicolumn{2}{|c|}{ Coordinates } & \multicolumn{3}{c|}{ Absolute Difference } & \multicolumn{3}{c|}{ Weight } \\ \hline i & ai & bi & (x1ai)2 & (y1bi)2 & (x2ai)2 & (y2bi)2 & w1i & w2i \\ \hline 1 & 0 & 10 & 0.00 & 100.00 & 0.00 & 100.00 & 10 & 0 \\ \hline 2 & 15 & 0 & 225.00 & 0.00 & 225.00 & 0.00 & 6 & 2 \\ \hline 3 & 25 & 30 & 625.00 & 900.00 & 625.00 & 900.00 & 0 & 16 \\ \hline 4 & 40 & 15 & 1600.00 & 225.00 & 1600.00 & 225.00 & 0 & 8 \\ \hline \end{tabular} 9 LOAD-DISTANCE FOR NEW LOCATIONS, x1 AND 2 DECISION VARIABLE FOR NEW LOCATION \begin{tabular}{c|c|c|c|c} \hline x1 & y1 & x2 & y2 & f(X) \\ \hline & & & & 41800 \\ \hline \end{tabular} 14 Three new facilities are to be located relative to six existing facilities. The weighting factors are vjk= flow intensity between new machines j and k, and wji= flow intensity between new machine j and existing machine i : The coordinate locations of the existing facilities are P1=(0,10),P2=(15,0),P3= (10,25),P4=(5,15),P5=(20,20), and P6=(25,5). a. Use the Excel WO SOLVER tool to solve the linear programming formulation of the minisum location problem assuming rectilinear distance. b. Use the Excel SOLVER tool to solve the minisum multifacility rectilinear location problem. c. Use the Excel SOLVER tool to solve the location problem assuming Euclidean distance. d. Solve the multifacility gravity