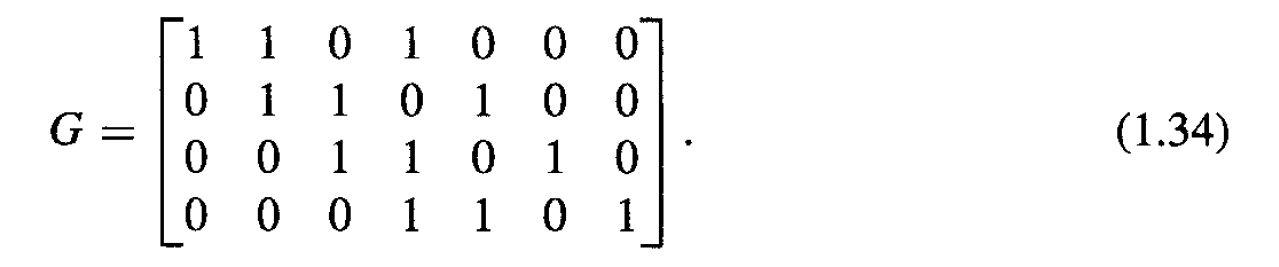
1.20 Hamming code decoding. (a) For G in (1.34) and H in (1.37), verify that GHT = 0. (Recall that operations are computed modulo 2.) (b) Let m = [1, 1, 0, 0]. Determine the transmitted Hamming codeword when the generator of (1.34) is used. (C) Let r = [1,1,1,1,1,0,0]. Using Algorithm 1.1, determine the transmitted codeword c. Also determine the transmitted message m. (d) The message m = [1,0,0,1) is encoded to form the codeword c = [1,1,0,0, 1, 0, 1). The vector r = [1,0,1,0,1,0,0] is received. Decode r to obtain . Is the codeword @ found the same as the original c? Why or why not? O 1 O 1 1 1 O 1 1 0 1 1 1 1 1 O (1.737) 1 1 0 G= 0 0 1 0 1 1 0 1 0 0 1 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 1 (1.34)