1,2,3,4

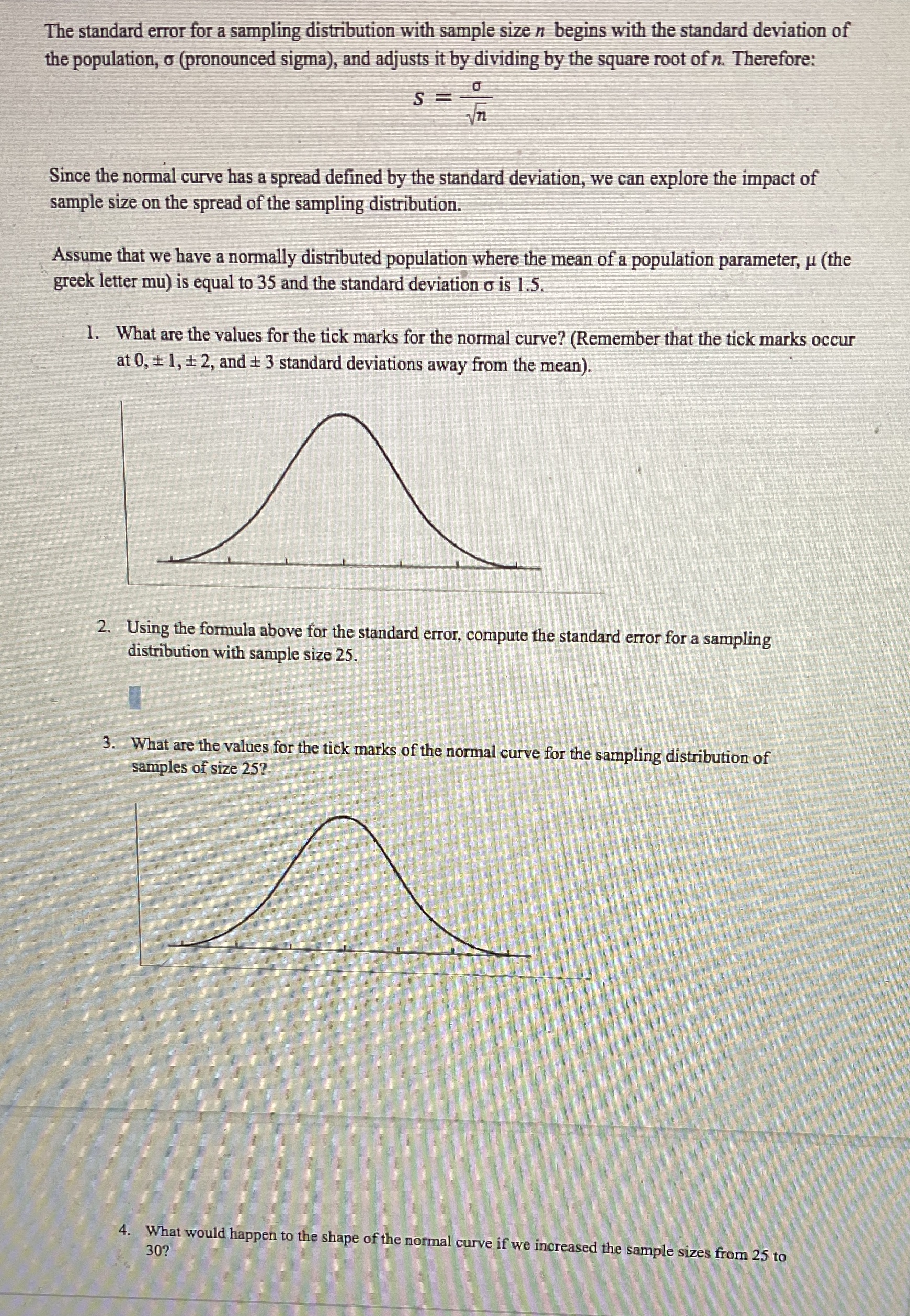
The standard error for a sampling distribution with sample size n begins with the standard deviation of the population, o (pronounced sigma), and adjusts it by dividing by the square root of n. Therefore: S = - Since the normal curve has a spread defined by the standard deviation, we can explore the impact of sample size on the spread of the sampling distribution, Assume that we have a normally distributed population where the mean of a population parameter, u (the greek letter mu) is equal to 35 and the standard deviation o is 1.5. 1. What are the values for the tick marks for the normal curve? (Remember that the tick marks occur at 0, + 1, # 2, and + 3 standard deviations away from the mean). 2. Using the formula above for the standard error, compute the standard error for a sampling distribution with sample size 25. 3. What are the values for the tick marks of the normal curve for the sampling distribution of samples of size 25? 30? 4. What would happen to the shape of the normal curve if we increased the sample sizes from 25 to