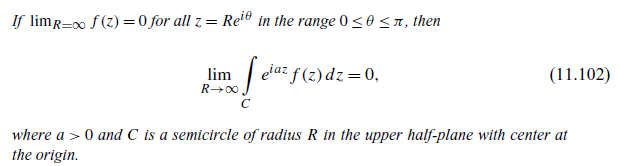
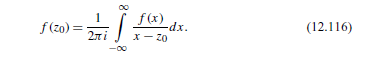
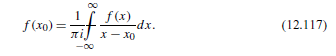
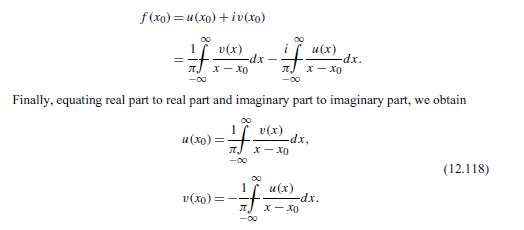
12.8.3 (a) The function f(z) = eiz does not vanish at the endpoints of the range of arg z, a and r. Show, with the help of Jordan's lemma, Eq. (11.102), that Eq. (12.116) still holds. (b) For f(z) = eiz verify by direct integration the dispersion relations, Eq. (12.117) or Eqs. (12.118). If limr= f(x)=0 for all z = Rel in the range 0 0 and C is a semicircle of radius R in the upper half-plane with center at the origin. f(20) = 21 i f(x) j dx . (12.116) X-20 f(x)=xit 1 - x0 1[ f(x) -dx. NI X- (12.117) f(x) = u(x0) +iv(xo) v(x) -dx X-XO u(x) dx. X-XO -oo Finally, equating real part to real part and imaginary part to imaginary part, we obtain (xo): V(x) -dx, X-XO (12.118) V(XO)=- JT u(x) dx. X-XO 12.8.3 (a) The function f(z) = eiz does not vanish at the endpoints of the range of arg z, a and r. Show, with the help of Jordan's lemma, Eq. (11.102), that Eq. (12.116) still holds. (b) For f(z) = eiz verify by direct integration the dispersion relations, Eq. (12.117) or Eqs. (12.118). If limr= f(x)=0 for all z = Rel in the range 0 0 and C is a semicircle of radius R in the upper half-plane with center at the origin. f(20) = 21 i f(x) j dx . (12.116) X-20 f(x)=xit 1 - x0 1[ f(x) -dx. NI X- (12.117) f(x) = u(x0) +iv(xo) v(x) -dx X-XO u(x) dx. X-XO -oo Finally, equating real part to real part and imaginary part to imaginary part, we obtain (xo): V(x) -dx, X-XO (12.118) V(XO)=- JT u(x) dx. X-XO