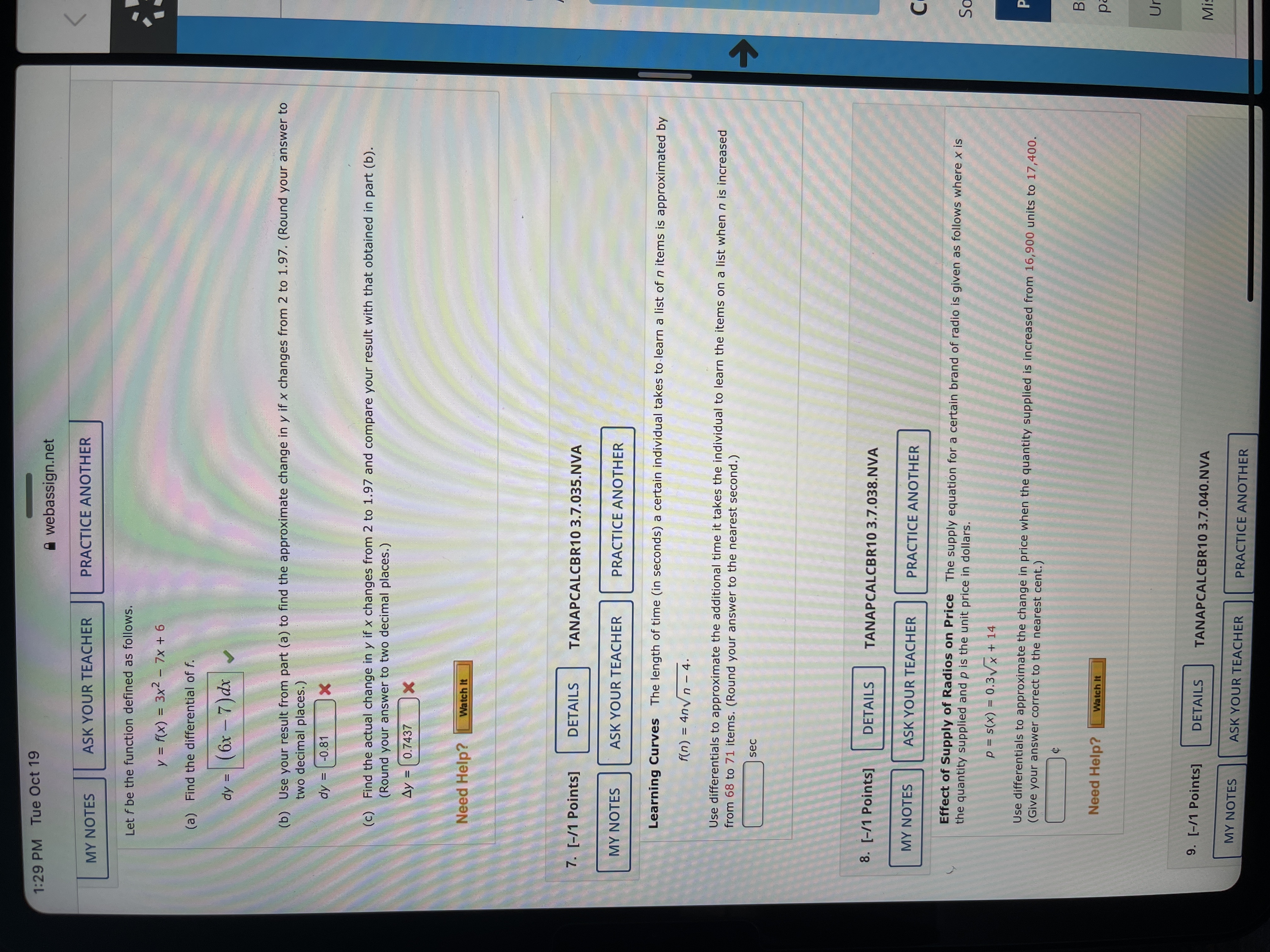
1:29 PM Tue Oct 19 webassign.net K MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Let f be the function defin ed as follows. y = f(x) = 3x2 -7x +6 (a) Find the differential of f. dy = (6x - 7) dx (b) Use your result from part (a) to find the approximate change in y if x changes from 2 to 1.97. (Round your answer to two decimal places.) dy = -0.81 X (c) Find the actual change in y if x changes from 2 to 1.97 and compare your result with that obtained in part (b). (Round your answer to two decimal places.) Ay = 0.7437 x Need Help? Watch It 7. [-/1 Points] DETAILS TANAPCALCBR10 3.7.035.NVA MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Learning Curves The length of time (in seconds) a certain individual takes to learn a list of n items is approximated by f (n ) = 4nvn - 4. Use differentials to approximate the additional time it takes the individual to learn the items on a list when n is increased from 68 to 71 items. (Round your answer to the nearest second.) sec 8. [-/1 Points] DETAILS TANAPCALCBR10 3.7.038.NVA MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Effect of Supply of Radios on Price The supply equation for a certain brand of radio is given as follows where x is the quantity supplied and p is the unit price in dollars. So P = s(x) = 0.3vx+ 14 Use differentials to approximate the change in price when the quantity supplied is increased from 16,900 units to 17,400. (Give your answer correct to the nearest cent.) Need Help? Watch It Ur 9. [-/1 Points] DETAILS TANAPCALCBR10 3.7.040.NVA Mi MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER