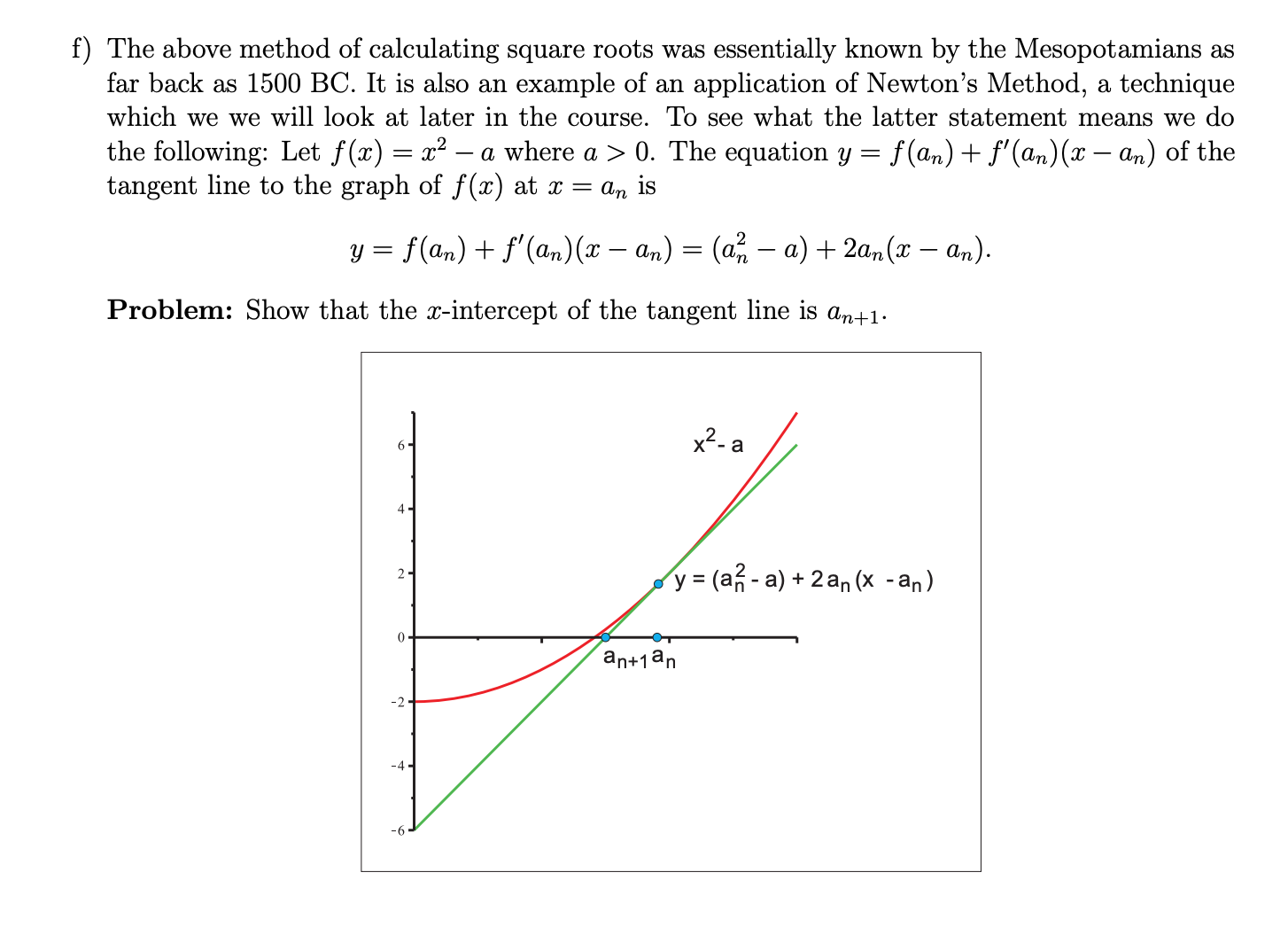
14) Calculating Square Roots: Herron's Method [24 Marks, 4 for each part] Let 05 >0. Let m =1 and mad 2 anPi) for all n E N. a) Use the Arithmetic Rules for Sequences to show that if {an} converges to L with L 75 0, then liIn an = J5. 11.4}00 (Note: It is easy to show by Induction that an > 0 for each n E N so yOu may use this fact without proof.) b) Show that an is a root of the polynomial 1971(3) = 2:2 2an+1m + a. c) Prove that that 4ai+14a20 and hence that \"3+1 2 '1 (*) forallnEN. d) Show that _ Mai - a) an _ an+1 2 (**) an and use this to show that the sequence an must converge. e) Let a=17. Let bn = an V17. Find (15 and b5. (Express your answer as a oating point number. That is as a decimal expression.) f) The above method of calculating square roots was essentially known by the MesOpotamians as far back as 1500 BC. It is also an example of an application of Newton's Method, a technique which we we will look at later in the course. To see what the latter statement means we do the following: Let f($) = 3:2 a where a > O. The equation y = flan) + f'(an)($ an) of the tangent line to the graph of f(:17) at a: 2 an is y = an) + f'(an)($ - an) = (031 - a) + 2%(2? - an)- Problem: Show that the zitintercept of the tangent line is an