Question: 14. Show that | sinh z|2 = sinh x + sin y, | cosh 2 2 = sinh x + cosy, and hence deduce that

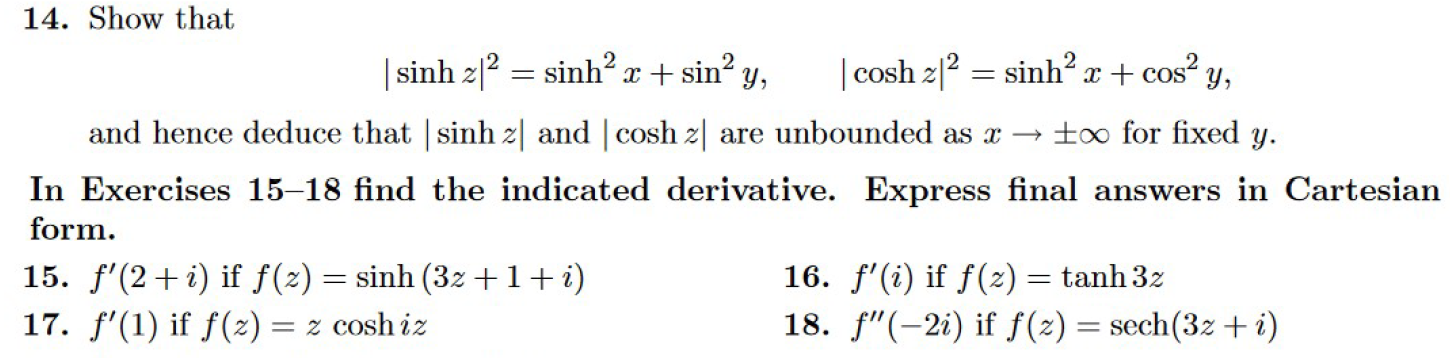
14. Show that | sinh z|2 = sinh x + sin y, | cosh 2 2 = sinh x + cosy, and hence deduce that | sinh z) and | cosh z] are unbounded as x - too for fixed y. In Exercises 15-18 find the indicated derivative. Express final answers in Cartesian form. 15. f'(2 + i) if f(2) = sinh (3z + 1 +2) 16. f'(i) if f(2) = tanh 3z 17. f'(1) if f( z) = z coshiz 18. f"(-2i) if f(z) = sech(3z + i)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

. A stream function is given by: y sin where L and K are constants, 0xL and y 0. a) Does y represent a potential flow, does it obey Laplace's equation? b) What are the velocity components Vx and vy?...

In Sec. 34, use expressions (13) and (14) to derive expressions (15) and (16) for |sin z|2 and |cos z|2. (13) sin z = sin x cosh y + i cos x sinh y, (14) cos z = cos x cosh y i sin x sinh y, where z...

= n a X 2 n 2 2 EnE 2 ma3. ( /24 pts) Suppose an infinite square well potential is given by c D (a) (4 pts) Sketch the potential. (b) (12 pts) As we saw in class, the general solution to the infinite...

5. /16 pts) A particle in a one-dimensional, infinite square well of length L has the initial, normalized wave function CO I (x, 0) = (a) (8 pts) Find I(x, t). (b) (4 pts) What is the probability of...

7/4/23, 11:16 PM Homework 8.7-Anh Nguyen Use a table of integrals to determine tv7t+ 19 at. Click here to view page 1 of the integral table. " Click here to view page 2 of the integral table. 14...

1 Multivariable functions and vector geometry Due date and time: Wednesday, June 7th at 9:30 AM in lecture Please ensure that you have read and understood the document \"Homework Guidelines" on the...

4. ( function /30 pts) This problem must be done without online integrators. A particle has the wave Y(x) = { Axe-Ax 0 0

The mode shape reported in Table 10.4 for a pinned-free beam of $\sqrt{3} x$ is a rigid-body mode. Indicate whether the statement presented is true or false. If true, state why. If false, rewrite...

Please help with 5 part question View History Bookmarks Profiles Tab Window Help 14 6 9 8 0 Tue Nov | Towson x | Content ta The Expert TA | Human-like ( x Problem 5: Consider the five x | +...

In Minkowski spacetime, the set of all events separated from the origin by a time like interval a 2 is a 3-surface, the hyperboloid t 2 x 2 y 2 z 2 = a 2 , where {t , x, y, z} are Lorentz...

0 PR 16-2A Statement of cash flows OBJ. 2,3,4,5 The comparative balance sheet of Orange Angel Enterprises Inc. at December 31, 20Y8 and 20Y7, is as follows: Dec. 31, 2018 Dec. 31, 2017 Assets...

On page 457 it was shown that for a spin echo applied to an I3S spin system the amount of the singly anti-phase terms goes as cos2 (2J ) sin (2J ). Maximizing this function is equivalent to finding...

12 Zara is putting numbers into a two-step function machine. Read what Zara says. When x=2, y=-4. As my x-values increase by 2, my y-values increase by 16. Work out the equation for Zara's function....

3. Oxy Inc. sells products with warranties included in the selling price. By law, Oxy is required to charge 8% sales tax. During October, Oxy sold $10,000 worth of products costing $8,000 for cash...