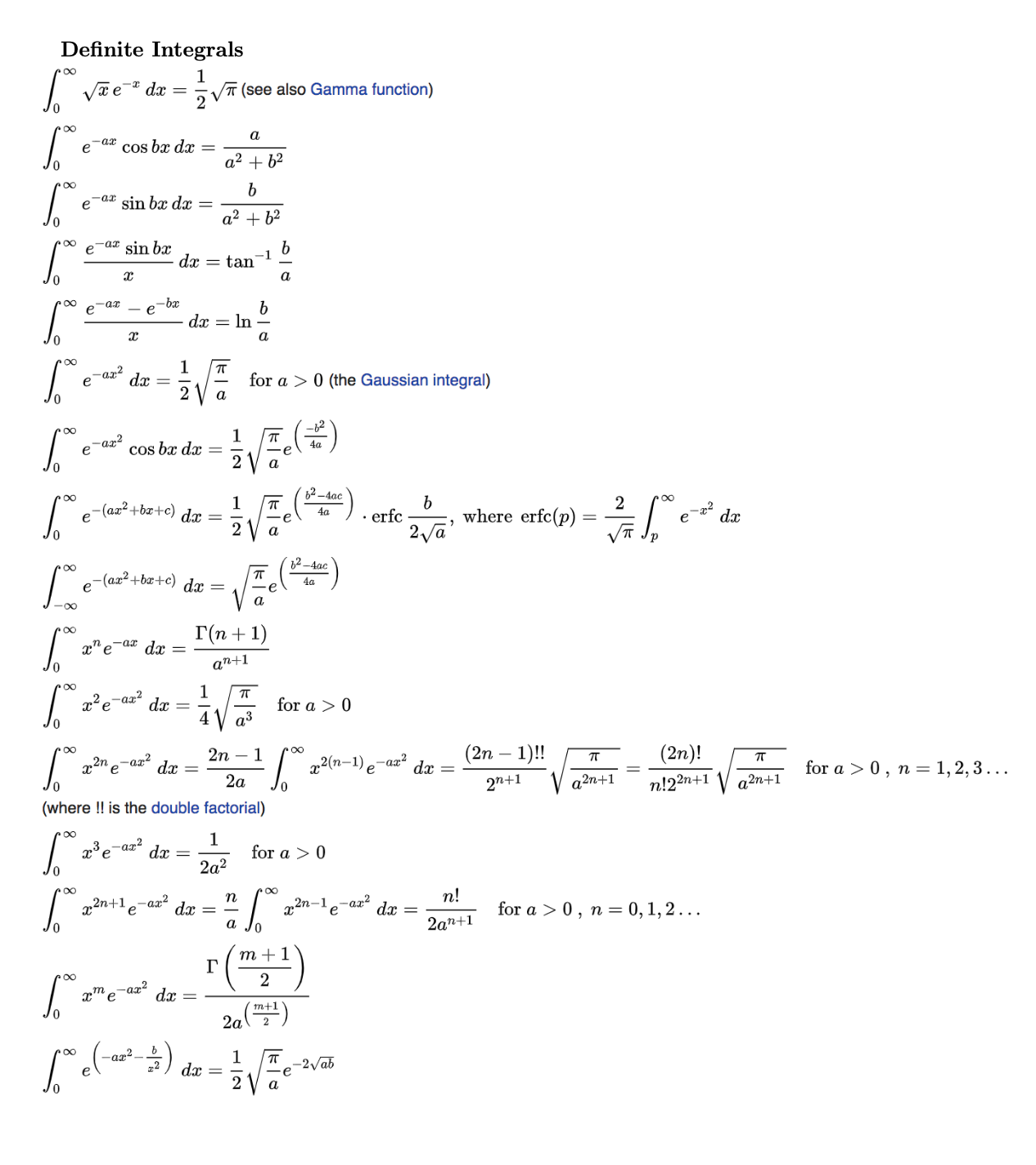
4. ( function /30 pts) This problem must be done without online integrators. A particle has the wave Y(x) = { Axe-Ax 0 0 < x x < 0, where A and are constants. (a) (4 pts) Normalize to find the constant A. (b) (4 pts) Find the expectation value of , (). (c) (3 pts) Find the expectation value of , (). (d) (4 pts) Find the expectation value of x, (^2). (e) (8 pts) Find the expectation value of p, (2). (f) (2 pts) Find the uncertainty in the value of x, x. (g) (2 pts) Find the uncertainty in the value of p, p. (h) (3 pts) Verify the uncertainty principle is satisfied. Helpful Integrals and Mathematical Relationships Commutator Relationships 1. [A+ B,C] = [A,C] + [B,C] 2. [A, A] = 0 3. [A, B] = [B, A] 4. [A, [B, C]] + [B, [C, A]] + [C, [A, B]] = 0 Gamma Functions T(n) = (n 1)!, and hence F(1) = 1, For positive half-integers, the function values are given ex (n-2)!! () = = T , n-1 22 or equivalently, for non-negative integer values of n: F(2) = 1, (3) = 2, (4) = 6, T(5) = 24, ( 1/1 + n) (2n-1)!! (2n)! = 2n I (-n) = (-2)" (2n-1)!! 4nn! (-4)"n! = (2n)! where n!! denotes the double factorial. In particular, T (/) = 5 T T 7|2 1.772 453 850 905 516 0273 == 0.886 226 925 452 758 0137 1.329 340 388 179 137 0205 = 153.323 350 970 447 842 5512 Definite Integrals Loo e dx Loo 0 L L 00 ax 1 2 e cos bx dx = e -ax sin bx dx -ax sin bx x T -bx v (see also Gamma function) a a + b b a +62 dx = tan-1 dx = ln b a b a e -ax2 1 dx = for a 0 (the Gaussian integral) | S 0 L S L S 00 e-(ax+bx+c) dx = -ax 1 e cos bx dx = -62 4a 2 a 62-4ac 1 b 2 4a e erfc where erfc(p) a 2a **** -22 e dx b2-4ac 4a e a -(ax+bx+c) dx = o da = x-ax e xn-ax e (n + 1) an+1 1 dx = for a > 0 4V a3 2n 1 dx = x2(n-1) -ax e dx = 2a 0 (2n-1)!! 2n+1 T (2n)! q2n+1 n!22n+1 a2n+1 for a > 0, n = 1, 2, 3 ... (where !! is the double factorial) S S 00 -ax e dx = -ax2 e 00 [ 22n+1 e -ax -ax. dx 1 2a2 n dx = = a for a > 0 x2n-1 r (m + 1 ) dx = 2a 2 m+1 1 T 2 a e -2ab e -ar dx = n! 2an+1 for a > 0, n = 0, 1, 2... Table of Integrals* Basic Forms Integrals with Logarithms 2 Vax + bdx = 1 xndx = x+1 n+1 15a (-262 +abx+3ax)ax+b (26) dx = In |x| dr Judu-uv-vdu 1 ax+b = dx = In | ax + b a Integrals of Rational Functions 1 (x + a) 2 (x + a)" dx = ! x(x + a)"dx = ! 1 1+x -- dx = = 1 x+a (x + a) n+1 n+1 (n + 1)(n+2) 5dx = tan-1 I (2) (1) S In axdxx lnax-x (42) In ax dx = 1 (43) x(ax + b)dx = 4a3/2 [(2ax + b)ax(ax+b) 2 (3) -6 In 1|ax+ +a(ax+ - b)|] (27) In (ax + b)dx = (x + 1) 1 In(ax+b) x, a 0 (44) (4) b x (ax + b)dx = - 62 + 12a 8ax 3 ] x (ax + b) In(x +a) dxx ln(x + a) + 2a tan- - 2x (45) + (5) 63 8a5/2 Inax + (ax+b) (28) In(x - a) dx = x ln(x - a) + aln x+a x-a 2x (46) -,n-1 (6) x a dx = 1 xx aa + a | In (ar (x+a)+((n+1)x a) (29) a xdx - zdr = +tan Va-z 1 1 1 dx = tan -1 a2x2 (9) a a I dx = ax dr+ In a + x2| (10) 2 -12 dx = xa tan ax (11) a dx = In 73 1 12 a + x dx = a In a + x2| (12) 2 1 dx = sin-1 (33) x2 a 2 dx = tan 4ac-6 2ax+b 4ac-62 (13) X dx = xa (34) 2 (30) + bx + c) dx = 1 4ac - 6 tan - 2x + (2 + z) In (az + bx + c) 2a x ln(ax + b)dx = 2a 4 -1 2ax+b 4ac-62 (47) bx 1 1 In (ax+b) +()I(a+b)(48) - 1 (x)/2 = In+ 2| (31) - x ln (a = bx) dx = x+ (32) (-)(-8) (19) Integrals with Exponentials (50) ax + bx + c 1 (x + a) (x + b) 1 dx = In a+x b-a b+x ab (14) dx a-x Val-dr = -a-82 (35) dx = (x+a)2 a ax +Ina+x| (15) | x F x^\ + *| c = x^\x - 1 -dx = In lax + bx + cl ax + bx + c 2a (36) b tan-1 a4ac-62 2ax + b 4ac-62 (16) Integrals with Roots Sv x = adx = x- =(x - a)/2 (17) dx = 2xa (18) 1 dx = -2a-x (19) Vax + bx + cdx = 4ac-b 8a3/2 b+2ax 4a 1 ax Jdx=" 1 dx = xe dr = + redz a where erf(x) = | ze"dz = (x-1)e" ze" d= (-)" 2a3/2 erf (iax), 2 dt (51) (52) e (53) ax + bx + c xe dx = (x-2x+2) e (54) In 2ax 2ax+b+2a(ax + bx+c) (37) 1 48a5/2 xx- adx = a(x a)/ + (x a)/ Vax + bdx - (0+2) Vaz + b = (20) (21) S 1 1 =dx = ax + bx + c Jaa 2 (ax+b)3/2 dx= (39) (ax+b)5/2 (22) 5a cardz = erf (ixa) (59) 2a X dx = (x+2a)xa (23) I 1 xa dx = ax + bx + c ax + bx + c Se a dx = erf (xa) 2a (60) x(a-x) -dx = x(a-x)-a tan (24) b 2a3/2 In 2ax+b+2a(ax + bx + c) (40) [xe -az 1 dx=- (61) 2a x-a ax + bx+c= (2ax + bx + c (-36+2abx+8a(c+ax)) +3(63-4abc) In 6+2ax +2ax + bx + c) (38) In |2ax + b + 2a (ax + bx + c) [2-(+) C= a a xe dx = (x-3x + 6x 6) e* Teax n dx = dx fred (57) a "e dr (-1)". dx = a an++n, -ax], where (a,x) = ta-edt (58) 69 2x pax (55) (56) () 4 V dx 1 (41) dx = dx = x(a+x) - a ln [x+x+a] (25) (a + x)3/2 a Va+x2 a+x (62) 2a Integrals with Trigonometric Functions 1 sec sec x dx = secx tan x + In secx+tan x (84) Se cos rdr = e (sin x + cos x) (106) 2 sin axdx = Cos ax (63) a sin 2ax sin axdx = S secx tan xdx = secx (85) Sebz eba cos axdx = 1 ba a+b2e (a sin ax + bcos ax) (107) (64) 2 4a sec o tan da = see a 2 (86) 1 S sin" axdx = ze" sin zdz = re* (cos 2 2 cos 2 + 2sin ) (108) 1 sec rtanxdr = sec x, n0 (87) n 1 1 n 3 cos ax 2Fi cos ax a 2 2 2' [az] (65) re cos dr = 2(x cos x - sin x + sin x) (109) 3 cos ax cos 3ax si S cscdr = ln |tan In cscx cot | +C (88) sin axdx=- (66) 4a 12a Integrals of Hyperbolic Functions 1 csc csc axdx = cot ax (89) cos axdx = sin ax (67) a /cos 1 cosh axdx = sinh ax (110) a cos axdx = sin 2ax + (68) csc adr == 1 1 cot x cscx+ 2 4a 2 In cscx cotx (90) So 1 cos axdx = - 1+p cos S 1 csc" rcot cdr = csc" x,n = 0 Se ea cosh bxdx = (91) n a(1+p) pax a 62 [a cosh bxb sinh bx] ab 1+p 1 3+p 2F1 cos 2 '2' 2 (69) 3 sin ax cos axdx = + 4a sin 3ax 12a (70) secx csc xdx = ln | tan x|| Products of Trigonometric Functions and Monomials (92) e2ax (111) + a=b 4a 2 1 sinh ardx = cosh ax (112) a S cos ar sin bxdx = cos[(a b)x] cos[(a+b)x] 2(a - b) 2(a+b) , ab S 2 cos cdr = cos 2+2 sin r (93) Sea ea sinh bxdx = (71) ax Cosaada = Cos ux+ -sinuc (94) a2 62 |bcoshbx + asinhbc] a/b a 2ax S sin ax cos bxdx = - sin[(2a - b)x] I (113) a=b 4a 2 4(2a - b) x cos xdx = 2x cos x + (x - 2) sin x (95) sin ba + 2b sin[(2a + b)x] 4(2a + b) (72) si sin a cos dr = 1 x cos axdx = 2x cos ax a 2 Sear tanh brdr = + sin ax (96) a3 sin x (73) (a+26) (a+2b) a 2F1 + 1,2+ 2b 2b 1 cos ax sin bxdx = cos[(2a - b)x] 4(2a - b) cos bx 2b | x" cosxdx = (i)"+ [F(n + 1, ix) +(-1)"T(n+1, ix)] a 2b 2F 1,1E, -e2b] ea 2 tan [e] ab (114) a = b (97) a cos[(2a + b)x] 4(2a + b) (74) tanh ac dc = In cosh ax (115) a 1 cosax sin axdx = - cos ax (75) ST" x" cosaxdx = (ia)" [(-1)T(n+1, iax) -(n + 1, ixa)] (98) S cos ax cosh bxdx = S x sin 2ax sin ax cos bxdx = sin[2(a - b)x] 1 [a sin ax cosh bx a +62 +bcos ac sinh b (116) 4 8a 16(a - b) S 2 sin rdt = 2cosx+sinx (99) sin 2bx sin[2(a + b)x] + (76) 8b 16(a+b) x cos ax x sin axdx= a sin ax a (100) cos ac sinh brder = 1 a + b [b cos ax cosh bx+ sin 4ax sin sin ax cos axdx = (77) a sin a sinh bc] (117) 8 32a St x sin xdx (2x2) cos x + 2x sin x (101) 1 tan axdx = - In cos ax (78) a sin ax cosh bxdx = S 1 tan axdx=-x+ tan ax (79) r sin axdx = 2-ax a3 cos ax + 2x sin ax a (102) 1 a + b bsin ar sinh br] -a cos ax cosh bx+ (118) tan" axdx = tan+1 ax a(1 + n) x sinrdr== = (i)" [F(n + 1, ix) (1)T(n+ 1, ix)] , 1, 2 2F (+11+-tanaz) 3 (103) ar (80) 2 sin a sinh brdr = 1 a + b a cos ar sinh br] [b cosh bx sin ax- (119) Products of Trigonometric Functions and S 1 1 tan axdx = In cos ax + sec ax 2a (81) Exponentials S sinh ax cosh axdx = 1 4a [2ax + sinh 2ax (120) 'sec ada=ln|sec x +tanz|=2tanh`(tan;) (82) se Se e sin rd = e (sin x cos x) (104) sinh ax cosh bxdx = /sec 1 axdx tan ax (83) eb sin axdx = a 1 eb (b sin axa cos ax) a+b (105) 1 62 - a -a cosh ax sinh bx] [b cosh bx sinh ax (121)