Question: 15. $mathrm{X}$ is $mathrm{N}left(mu_{1}, sigma^{2} ight)$ and $mathrm{Y}$ is $mathrm{N}left(mu_{2}, sigma^{2} ight) $ and let $mathrm{Z}=mathrm{X}+mathrm{Y}$, then the distribution of $mathrm{Z} $ is: $mathrm{N}$ 16.

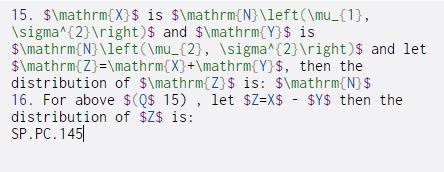
$15. $\mathrm{X}$ is $\mathrm{N}\left(\mu_{1}, \sigma^{2} ight)$ and $\mathrm{Y}$ is $\mathrm{N}\left(\mu_{2}, \sigma^{2}$

15. $\mathrm{X}$ is $\mathrm{N}\left(\mu_{1}, \sigma^{2} ight)$ and $\mathrm{Y}$ is $\mathrm{N}\left(\mu_{2}, \sigma^{2} ight) $ and let $\mathrm{Z}=\mathrm{X}+\mathrm{Y}$, then the distribution of $\mathrm{Z} $ is: $\mathrm{N}$ 16. For above $(Q$ 15), let $2=X$ - $Y$ then the ( distribution of $Z$ is: SP.PC. 145

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Following are the consolidated balance sheet accounts of Primer Inc. and its subsidiary, Sore Corporation, as of December 31, 20X6 and 20X5. Additional Information 1. On January 20, 20X6, Primer...

**Python Language can I get help? **below might help Programming Problem Modify your previous lab to do the following: 1. Using Python, work Ex 9.4 in the lecture notes (Lecture #31, Page 301). Use...

**Python Language can I get help? **bellow might help Programming Problem Modify your previous lab to do the following: 1. Using Python, work Ex 9.4 in the lecture notes (Lecture #31, Page 301). Use...

**Python Language can I get help? Programming Problem Modify your previous lab to do the following: 1. Using Python, work Ex 9.4 in the lecture notes (Lecture #31, Page 301). Use to = 8 [ms] and f =...

Rondelli Companys internal controls over cash disbursements provide for the treasurer to sign checks imprinted by a checkwriter after comparing the check with the approved invoice. Identify the...

12.27 The paper Overweight Among Low-Income Preschool Children Associated with the Consumption of Sweet Drinks (Pediatrics [2005]: 223229) described a study of children who were underweight or normal...

I dont trust that theyll keep my complaint confi dential.

Sunny Day Stores operates convenience stores throughout much of the United States. The industry is highly competitive, with low profit margins. The companys competition includes national, regional,...

Without any build in methods Assessment 1 (File Input & Output) Write a java program that: 1. Create a file with the name "ItemPrice.txt" and has the following content (the item name, first price and...

Figure shows a thermodynamic cycle on an ST diagram. Identify this cycle and sketch it on a PVdiagram. D.

We need to calculate the present value (the value at time period 0) of receiving a single amount of $1,000 in 20 years. The interest rate for discounting the future amount is estimated at 10% per...

Problem 6 - 2 0 Interest Rate Risk [ lO 2 ] Bond J has a coupon rate of 5 . 2 percent. Bond K has a coupon rate of 1 5 . 2 percent. Both bonds have ten years to maturity, a par value of $ 1 , 0 0 0 ,...

For the year, ABC ltd has direct materials of $30,000, direct labor of $10,000, manufacturing overhead of $20,000. The beginning work in process inventory of $5,000, and ending work in process...

14-3 How can firms assess the business value of information systems?

14-1 What are the objectives of project management, and why is it so essential in developing information systems?

14-4 What are the principal risk factors in information systems projects, and how can they be managed?