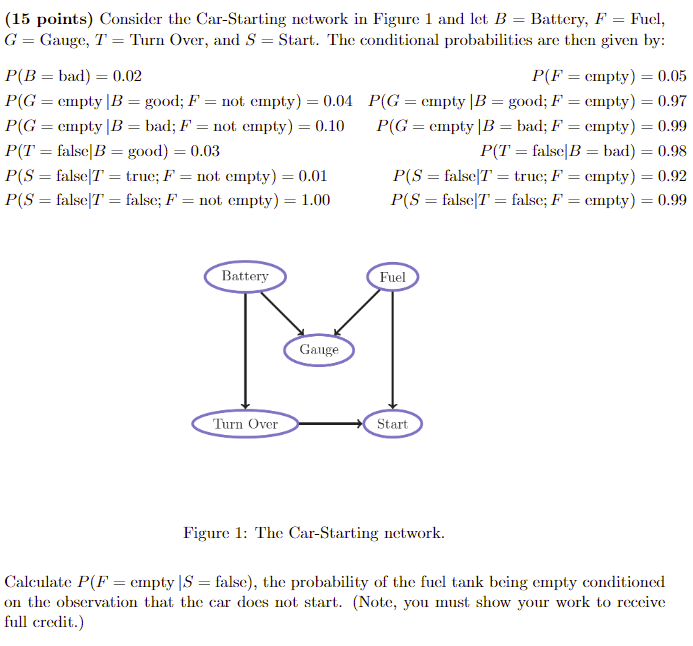
(15 points) Consider the Car-Starting network in Figure 1 and let B = Battery, F = Fuel, G = Gauge, T = Turn Over, and S = Start. The conditional probabilities are then given by: P(B bad)=0.02 = = P(F empty)=0.05 = = P(G=empty |B = good; F = not empty)=0.04 P(G= empty |B = good; F = empty) = 0.97 P(G empty |B = bad; F empty) = 0.99 P(T=false|B= bad) = 0.98 P(G=empty |B = bad; F = not empty) = 0.10 P(T=false|B= good) = 0.03 P(S=false|T = true; F = not empty) = 0.01 P(S=false|T = false; F = not empty) = 1.00 P(S=false|T = true; F = empty) = 0.92 P(S=false|T = false; F = empty) = 0.99 Battery Gauge Fuel Turn Over Start Figure 1: The Car-Starting network. Calculate P(F = empty |S = false), the probability of the fuel tank being empty conditioned on the observation that the car does not start. (Note, you must show your work to receive full credit.)