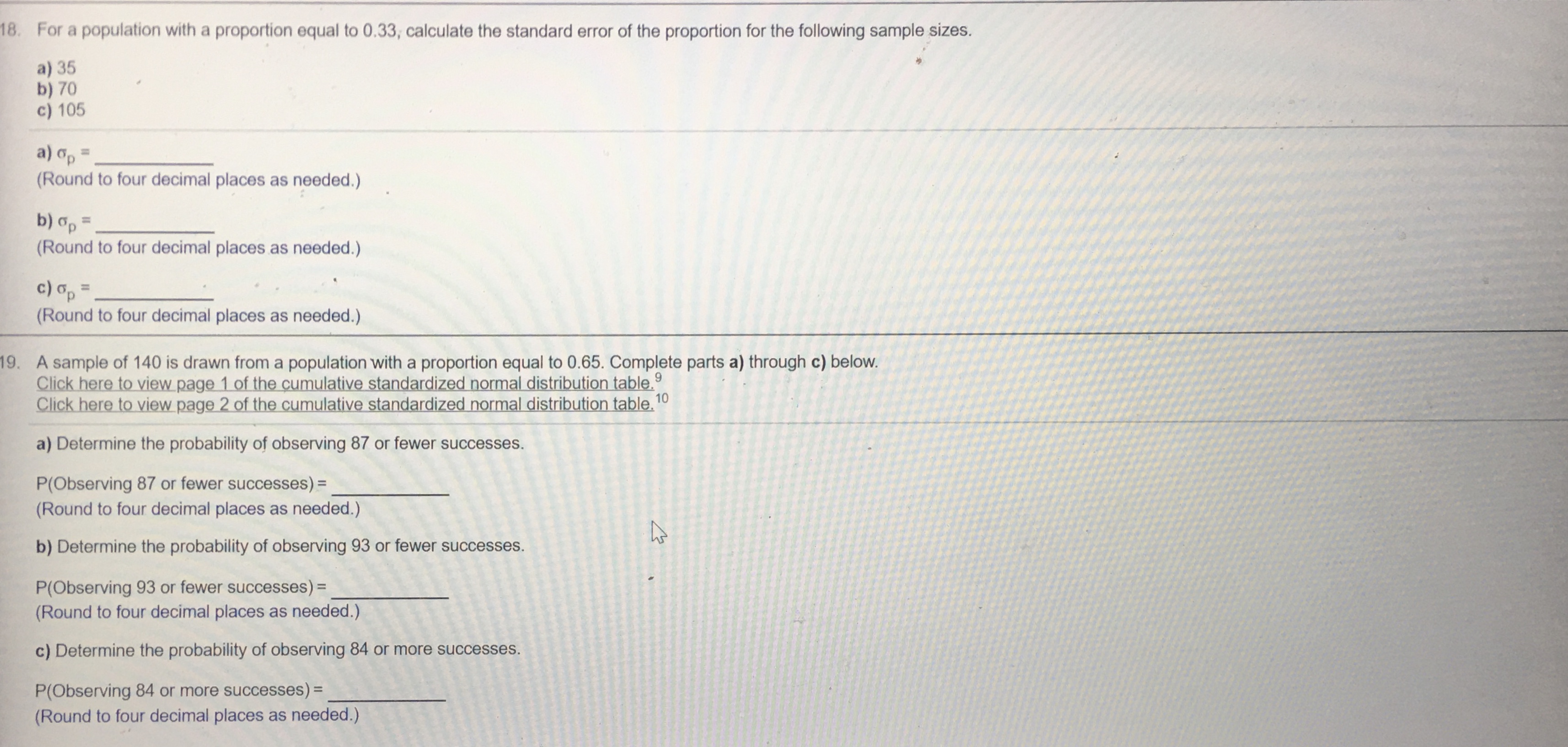
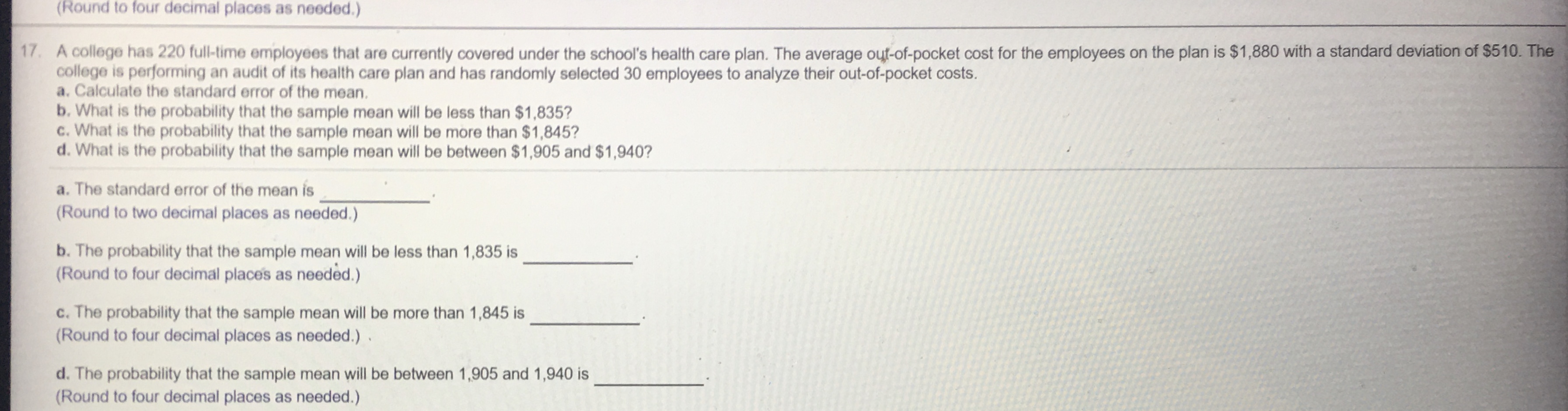
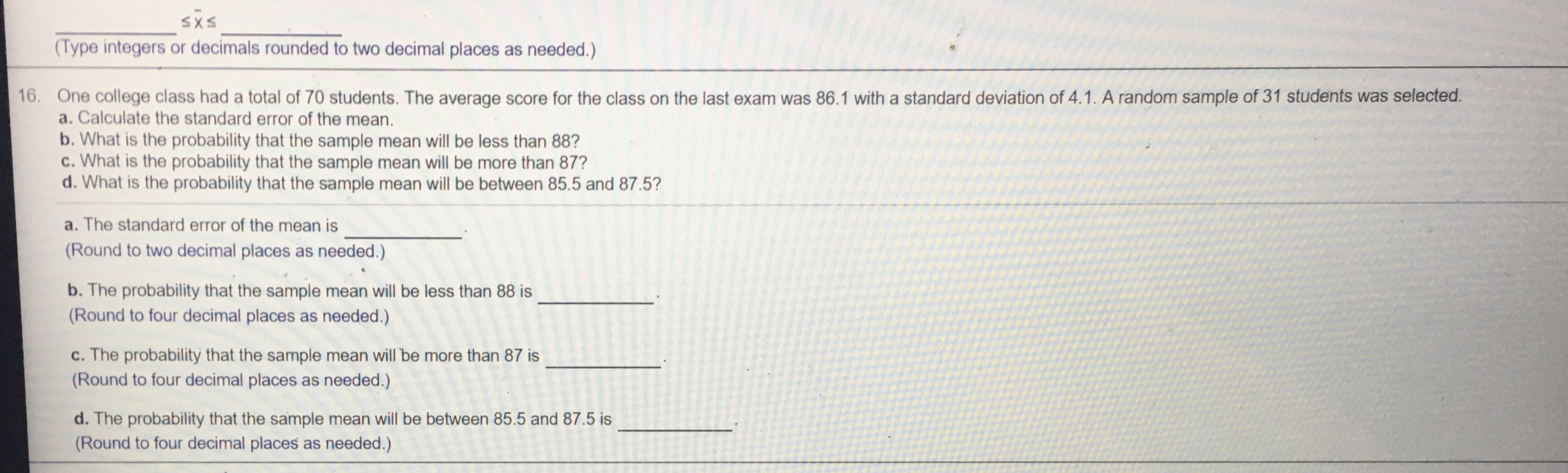
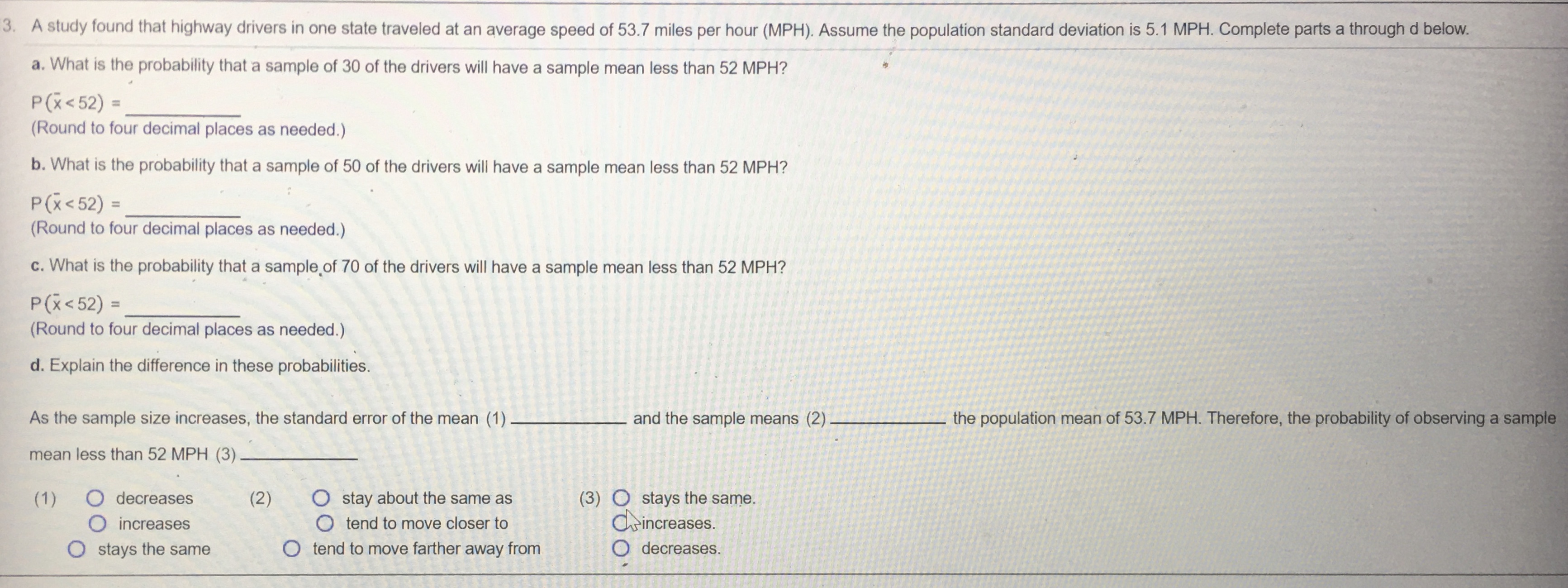
18. For a population with a proportion equal to 0.33, calculate the standard error of the proportion for the following sample sizes. a) 35 b) 70 c) 105 a) op = (Round to four decimal places as needed.) b) op = (Round to four decimal places as needed.) c ) op = (Round to four decimal places as needed.) 9. A sample of 140 is drawn from a population with a proportion equal to 0.65. Complete parts a) through c) below. Click here to view page 1 of the cumulative standardized normal distribution table." Click here to view page 2 of the cumulative standardized normal distribution table. 10 a) Determine the probability of observing 87 or fewer successes. P(Observing 87 or fewer successes) = (Round to four decimal places as needed.) b) Determine the probability of observing 93 or fewer successes. hs P(Observing 93 or fewer successes) = (Round to four decimal places as needed.) c) Determine the probability of observing 84 or more successes. P(Observing 84 or more successes) = (Round to four decimal places as needed.)(Round to four decimal places as needed.) 17. A college has 220 full-time employees that are currently covered under the school's health care plan. The average out-of-pocket cost for the employees on the plan is $1,880 with a standard deviation of $510. The college is performing an audit of its health care plan and has randomly selected 30 employees to analyze their out-of-pocket costs. a. Calculate the standard error of the mean. b. What is the probability that the sample mean will be less than $1,835? c. What is the probability that the sample mean will be more than $1,845? d. What is the probability that the sample mean will be between $1,905 and $1,940? a. The standard error of the mean is (Round to two decimal places as needed.) b. The probability that the sample mean will be less than 1,835 is (Round to four decimal places as needed.) c. The probability that the sample mean will be more than 1,845 is (Round to four decimal places as needed.) . d. The probability that the sample mean will be between 1,905 and 1,940 is (Round to four decimal places as needed.)SXS (Type integers or decimals rounded to two decimal places as needed.) 16. One college class had a total of 70 students. The average score for the class on the last exam was 86.1 with a standard deviation of 4.1. A random sample of 31 students was selected. a. Calculate the standard error of the mean. b. What is the probability that the sample mean will be less than 88? c. What is the probability that the sample mean will be more than 87? d. What is the probability that the sample mean will be between 85.5 and 87.5? a. The standard error of the mean is (Round to two decimal places as needed.) b. The probability that the sample mean will be less than 88 is (Round to four decimal places as needed.) c. The probability that the sample mean will be more than 87 is (Round to four decimal places as needed.) d. The probability that the sample mean will be between 85.5 and 87.5 is (Round to four decimal places as needed.)15. A pizza shop claims its average home delivery time is 26 minutes. A sample of 45 deliveries had a sample average of 28.7 minutes. Assume the population standard deviation for the shop's deliveries is 7.7 minutes. Complete parts a and b below. a. Is there support for the shop's claim using the criteria that the sample average of 28.7 minutes falls within the symmetrical interval that includes 95% of the sample means if the true population mean is 26 minutes? Select the correct choice below and fill in the answer box within your choice. (Type an integer or decimal rounded to four decimal places as needed.) O A. The probability P (x 2 28.7) This indicates that the sample average of 28.7 minutes falls outside the 95% symmetrical interval, contradicting the shop's claim. O B. The probability P (x 2 28.7) = This indicates that the sample average of 28.7 minutes falls within the 95% symmetrical interval, supporting the shop's claim. b. Identify the symmetrical interval that includes 95% of the sample means if the true population mean is 26 minutes. SXs (Type integers or decimals rounded to two decimal places as needed.) sample of 31 students was selected.14. The average weight of a professional football player in 2009 was 245.9 pounds. Assume the population standard deviation is 30 pounds. A random sample of 34 professional football players was selected. Complete parts a through e. a. Calculate the standard error of the mean. o- = (Round to two decimal places as needed.) b. What is the probability that the sample mean will be less than 239 pounds? P (x 243) = (Round to four decimal places as needed.) d. What is the probability that the sample mean will be between 253 pounds and 258 pounds? P (253 s x s 258) = (Round to four decimal places as needed.) e. Identify the symmetrical interval that includes 95% of the sample means if the true population mean is 245.9 pounds. SXs (Round to the nearest pound as needed.) minutes. A sample of 45 deliveries had a sample average of 28.7 minutes. Assume the population standard deviation for the shop's deliveries is 7.73. A study found that highway drivers in one state traveled at an average speed of 53.7 miles per hour (MPH). Assume the population standard deviation is 5.1 MPH. Complete parts a through d below. a. What is the probability that a sample of 30 of the drivers will have a sample mean less than 52 MPH? P (x 5.5) = (Round to four decimal places as needed.) Does this result support the findings of the study? The probability is (1) than 0.05, which means the result (2) the findings of the study. (1) O less (2) O does not support O greater O supports through d below.11. A professional baseball pitcher takes 15.58 seconds to throw each pitch, on average. Assume the pitcher's times per pitch follow the normal probability distribution with a standard deviation of 2.8 seconds. Complete parts a through d. a. What is the probability that a random sample of 15 pitches from this pitcher will have a mean less than 15 seconds? P (x