Please see below:

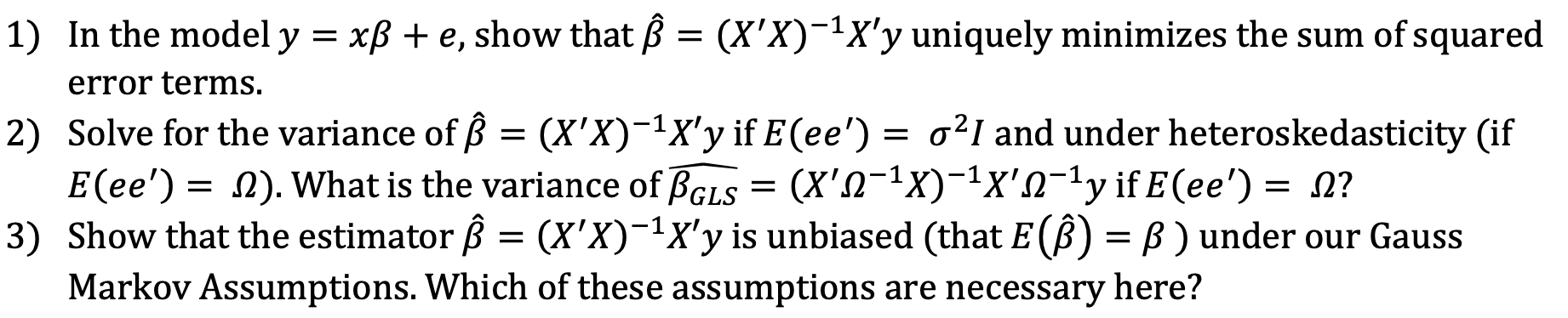
1) In the model y = xB + e, show that B = (X'X)-1X'y uniquely minimizes the sum of squared error terms. 2) Solve for the variance of B = (X'X)-1X'y if E(ee') = 2/ and under heteroskedasticity (if E(ee') = 0). What is the variance of BGLS = (X'n -1X) -1X'n ly if E(ee') = n? 3) Show that the estimator B = (X'X)-1X'y is unbiased (that E (B) = B ) under our Gauss Markov Assumptions. Which of these assumptions are necessary here