1.Assume that a competitive firm has the total cost function:

TC=1q3-40q2+870q+1500

Suppose the price of the firm's output (sold in integer units) is $700 per unit.

Using calculus and formulas (but no tables and restricting your use of spreadsheets to implementing the quadratic formula) to find a solution, how many units should the firm produce to maximize profit?

Please specify your answer as an integer.

Hint:The first derivative of the total cost function is the marginal cost function.

Set the marginal cost equal to the marginal revenue (price in this case) to define an equation for the optimal quantity q.

Rearrange the equation to the quadratic form aq2+ bq + c = 0, where a, b, and c are constants.

Use the quadratic formula to solve for q:

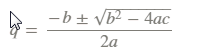
\f