Question: 1c. Please mathematically show how the continuous compounding formula can be derived in terms of the discrete compounding formula. 1d. Please discuss how the continuous

1c. Please mathematically show how the continuous compounding formula can be derived in terms of the discrete compounding formula.

1d. Please discuss how the continuous compounding formula can be used to estimate the growth rate.

1e. If we have the variance-covariance matrix for time, EPS, DPS, PPS, nature log EPS, nature log DPS, and nature log PPS as follows. Please calculate the growth rate of EPS, DPS, and PPS in terms of a continuous compounding regression model.

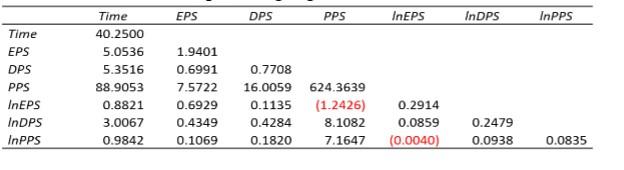
1c. Please mathematically show how the continuous compounding formula can be derived

\begin{tabular}{lrrrrrrr} \hline & \multicolumn{1}{c}{ Time } & EPS & DPS & \multicolumn{1}{c}{ PPS } & \multicolumn{1}{c}{lnEPS} & lnDPS \\ \hline Time & 40.2500 & & & & & \\ EPS & 5.0536 & 1.9401 & & & & \\ DPS & 5.3516 & 0.6991 & 0.7708 & & & \\ PPS & 88.9053 & 7.5722 & 16.0059 & 624.3639 & & \\ InEPS & 0.8821 & 0.6929 & 0.1135 & (1.2426) & 0.2914 & \\ InDPS & 3.0067 & 0.4349 & 0.4284 & 8.1082 & 0.0859 & 0.2479 \\ InPPS & 0.9842 & 0.1069 & 0.1820 & 7.1647 & (0.0040) & 0.0938 & 0.0835 \\ \hline \end{tabular} \begin{tabular}{lrrrrrrr} \hline & \multicolumn{1}{c}{ Time } & EPS & DPS & \multicolumn{1}{c}{ PPS } & \multicolumn{1}{c}{lnEPS} & lnDPS \\ \hline Time & 40.2500 & & & & & \\ EPS & 5.0536 & 1.9401 & & & & \\ DPS & 5.3516 & 0.6991 & 0.7708 & & & \\ PPS & 88.9053 & 7.5722 & 16.0059 & 624.3639 & & \\ InEPS & 0.8821 & 0.6929 & 0.1135 & (1.2426) & 0.2914 & \\ InDPS & 3.0067 & 0.4349 & 0.4284 & 8.1082 & 0.0859 & 0.2479 \\ InPPS & 0.9842 & 0.1069 & 0.1820 & 7.1647 & (0.0040) & 0.0938 & 0.0835 \\ \hline \end{tabular}

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Finance Questions!

Need the answer in Java Language!!! Programming Project-3 In this project you will write a program that perform certain financial calculations. The financial calculations should be done in methods....

Planning Demand and Supply in a Supply Chain Capacity Planning and Assignment 1 utdallas.edu/~metin Outline Capacity Planning Product-to-plant Assignment utdallas.edu/~metin 2 Deterministic Capacity...

Java Language Programming Project-3 In this project you will write a program that perform certain financial calculations. The financial calculations should be done in methods. Do sections A B and C...

Java Programming Project-3 In this project you will write a program that perform certain financial calculations. The financial calculations should be done in methods. Do sections A B and C in one...

DSP First Lab 1 (Chapters 2 and 3) handoutThis is an individual lab report which will be graded by answering each of the following questions. Please submit a MATLAB script (.m file) that will do each...

Can you please help me by showing the code in matlab and mathematically how to solve it? please read over the following to complete this. This must have the following components: 1) Clearly Defined...

please help to my homework SUMMARY OF FORMULA (Discrete Compounding Interest Factors and Symbols) To Given: Factor by which to Factor Name Factor Functional find: multiply Symbol For Single Cash...

now//You are asked to price some options on KYC stock. KYC's stock price can go up by 15 percent every year, or down by 10 percent. Both outcomes are equally likely. The risk free rate is 5 percent,...

Macro...solve all the following 1.5 Options 1. A stock price is currently $50. It is known that at the end of two months it will be either $53 or $48. The risk-free interest rate is 10% per annum...

Java Programming Project 3 Programming Project-3 In this project you will write a program that perform certain financial calculations. The financial calculations should be done in methods. Do...

Using the earnings data given in Exercise 10.3, determine the amount of Medicare tax to be withheld from each employees gross pay for December. Assume a 1.45 percent Medicare tax rate and that all...

Which of the following is the better chemical for removing calcium ions from water? Make sure you show the calculations necessary to justify your answer. For this problem, ignore calcium complexes....

Explain which of the following expressions have semantic meaning and which do not:

9. (15 points) A company is considering a new project that requires an investment of \$5 million. The project is expected to generate cash flows of $2 million in year 1,$3 million in year 2, and $4...

Technology. Attend a career fair or visit your campus career center and gather information on jobs available in your field. Send an e-mail to your instructor listing five possible positions for which...

Comment on what is incorrect, incomplete, or inappropriate in the following rsum sections. Rewrite each section to make it stronger, adding material where appropriate. Follow the rsum guidelines that...

How do you address an application letter if you are replying to a classified ad that does not list a contact person? (Objective 1)