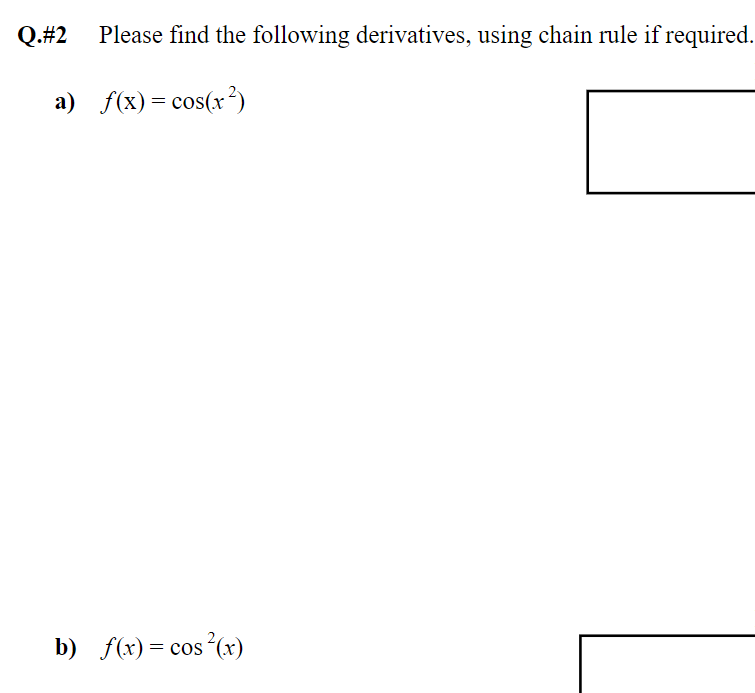
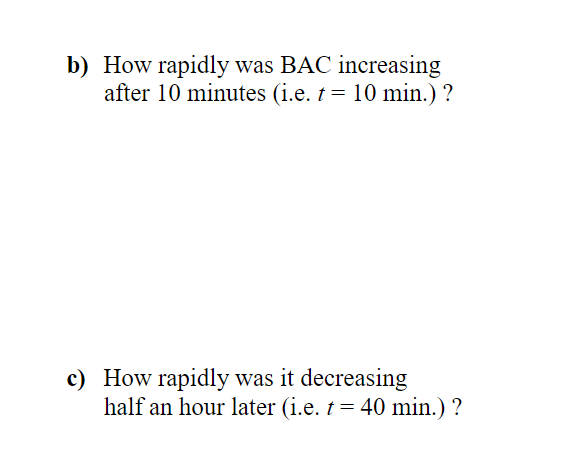
1-x Q. #231 Given f(x)=- " please find derivatives below. 1+x Hint: Always simplify between derivatives! a) f'(x) b) f"(x) c) f"(x) Q.#2 Please find the following derivatives, using chain rule if required. a) f(x) = cos(x) b) f(x) = cos(x) c) f(x) = sin x cos x d) f(x)=sin(cos.x) Q.#5 Using derivative rules (NOT definition of the derivative), prove that (secx)' = sec x tan x. Hint: Similar to proof that (tan x)' = sec x from A#2, also remember secx = 1/cosx = (cosx) The average blood alcohol concentration (BAC) of 8 male subjects was measured after consuming 15 ml of ethanol (i.e. one drink). The results modeled by this consumption function: C(t)=0.0225te 0.0467t where t is time after alcohol consumption in minutes, and C(t) is alcohol concentration in blood in mg/ml Using the above, please answer the following. a) What is the derivative of C(t), namely C'(t) ? Final Answer b) How rapidly was BAC increasing after 10 minutes (i.e. t = 10 min.)? c) How rapidly was it decreasing half an hour later (i.e. t = 40 min.)?