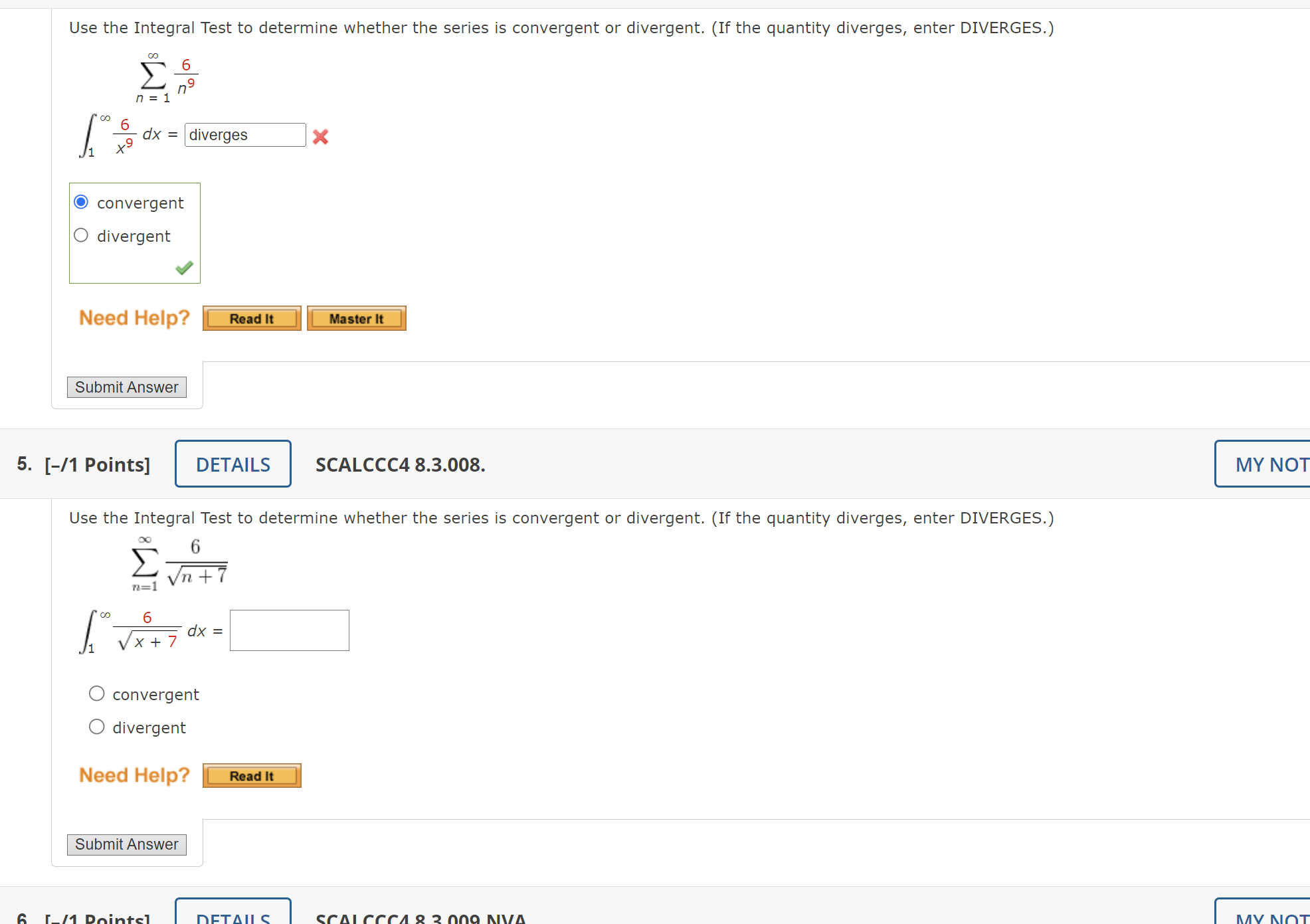
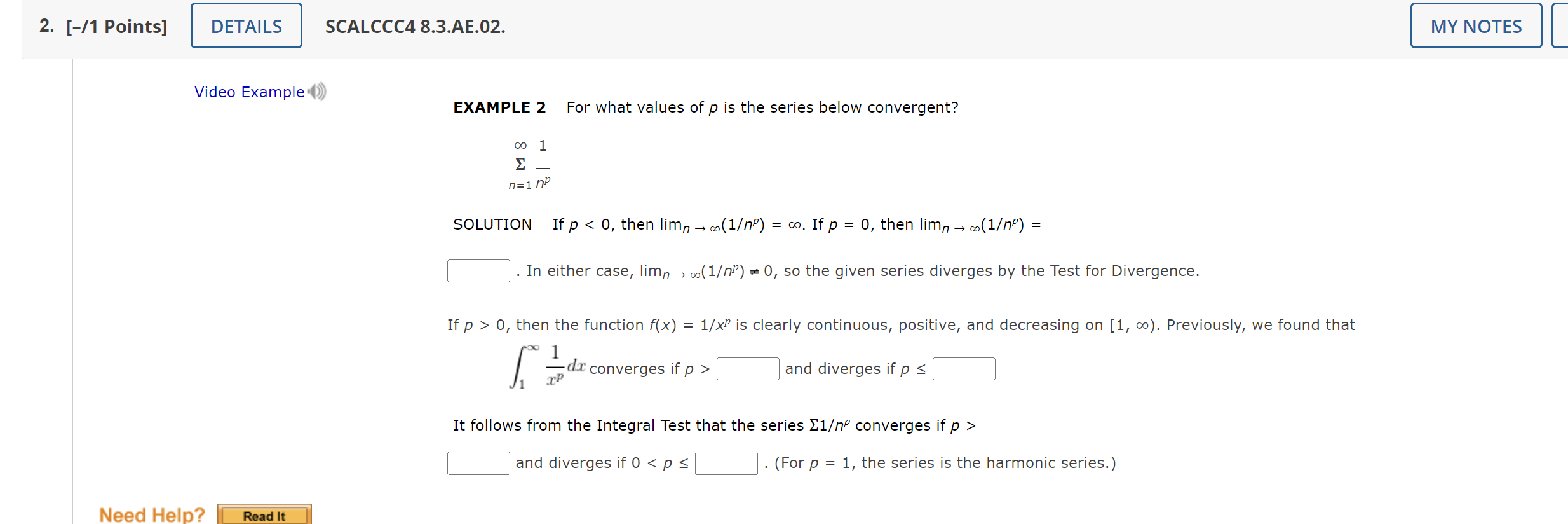
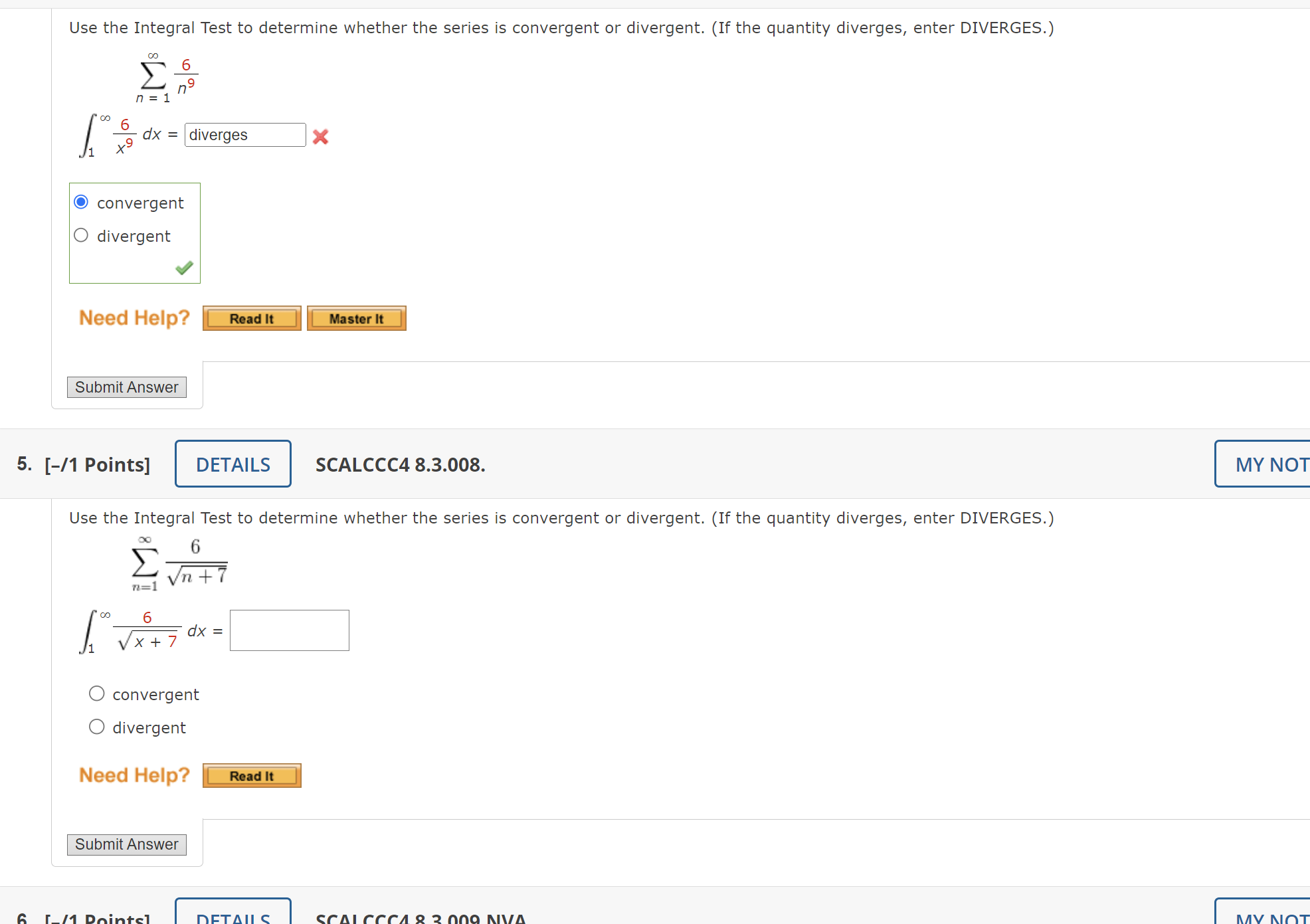
2. [-/1 Points] DETAILS SCALCCC4 8.3.AE.02. MY NOTES Video Example () EXAMPLE 2 For what values of p is the series below convergent? 00 1 E n=1 np SOLUTION If p co(1P) = co. If p = 0, then limn - co(1p) = . In either case, limn -> co(1P) = 0, so the given series diverges by the Test for Divergence. If p > 0, then the function f(x) = 1/xP is clearly continuous, positive, and decreasing on [1, co). Previously, we found that di converges if p > and diverges if p s It follows from the Integral Test that the series X1P converges if p > and diverges if 0