$2.(24$ points$)$ Consider building a B$+-$tree to store numbers. You are given the following constraints on the $\backslash (\backslash$mathrm$\{$B$\}+\backslash )-$tree.

$-$ Each leaf node can store at most $4$ numbers

$-$ Each internal node can store at most $2$ numbers $($how many children maximum?$)$

$-$ Suppose an internal node store $\backslash ((14,28)\backslash ).$ The three children correspond to number with value strictly less than $14,$ greater than or equal $14$ and strictly less than $28,$ and greater than or equal to $28$ respectively.

$-$ If a node is split, and the number of items of the nodes are odd $-$ this implies one of the split nodes will have one more item than the other. In such case choose the node on the "right" $($containing larger numbers$)$ to be the one who get one more item.

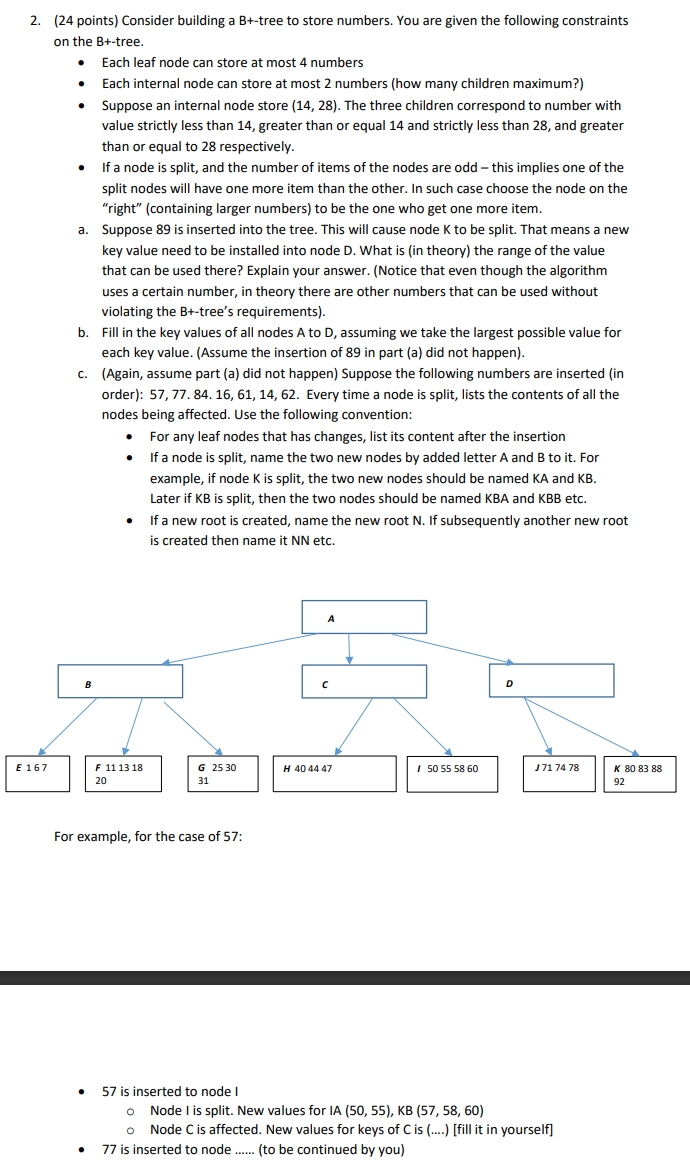
a$.$ Suppose $89$ is inserted into the tree. This will cause node K to be split. That means a new key value need to be installed into node D $.$ What is $($in theory$)$ the range of the value that can be used there? Explain your answer. $($Notice that even though the algorithm uses a certain number, in theory there are other numbers that can be used without violating the $\backslash (\backslash$mathrm$\{$B$\}+\backslash )-$tree's requirements$).$

b$.$ Fill in the key values of all nodes $\backslash ($ A $\backslash )$ to $\backslash ($ D $\backslash ),$ assuming we take the largest possible value for each key value. $($Assume the insertion of $89$ in part $($a$)$ did not happen$).$

c$.($Again$,$ assume part $($a$)$ did not happen$)$ Suppose the following numbers are inserted $($in order$)$: $\backslash (57,77\mathrm{.}84\mathrm{.}16,61,14,62\backslash ).$ Every time a node is split, lists the contents of all the nodes being affected. Use the following convention:

$-$ For any leaf nodes that has changes, list its content after the insertion

$-$ If a node is split, name the two new nodes by added letter $\backslash ($ A $\backslash )$ and $\backslash ($ B $\backslash )$ to it$.$ For example, if node $\backslash ($ K $\backslash )$ is split, the two new nodes should be named KA and KB$.$ Later if KB is split, then the two nodes should be named KBA and KBB etc.

$-$ If a new root is created, name the new root N $.$ If subsequently another new root is created then name it NN etc.

$-57$ is inserted to node I

$-$ Node I is split. New values for IA $\backslash ((50,55)\backslash ),$ KB $\backslash ((57,58,60)\backslash )$

$-$ Node C is affected. New values for keys of C is $(....)[$fill it in yourself$]$

$-77$ is inserted to node $......($to be continued by you$)$